安徽省2022-2023学年八年级上学期期末教学质量检测数学试卷

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，若点 $P (- 2 ， x)$ 在第二象限，则x是（）

A、正数 B、负数 C、正数或0 D、任意数

查看试题解析
2. 如图所示，图中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $△ A B C$ 中， $A B = 3$ ， $B C = 4$ ，则第三边AC的取值范围是（）

A、 $3 < A C < 4$ B、 $0 < A C < 12$ C、 $1 \leq A C \leq 7$ D、 $1 < A C < 7$

查看试题解析
4. 如图，若 $△ A B C ≌ △ D E F$ ，则 $∠ D$ 等于（）

A、 $30 °$ B、 $50 °$ C、 $60 °$ D、 $100 °$

查看试题解析
5. 下列命题中，假命题是（）

A、全等三角形对应角相等 B、对顶角相等 C、同位角相等 D、有两边对应相等的直角三角形全等

查看试题解析
6. 如图， $B E$ 是 $△ A B C$ 的外角 $∠ C B D$ 的平分线，若 $∠ C = 75 °$ ， $∠ E B D = 60 °$ ，则 $∠ A =$ （）

A、35° B、40° C、45° D、55°

查看试题解析
7. 点 $A (m ， y_{1})$ 、 $B (m + 1 ， y_{2})$ 都在直线 $y = - \frac{1}{4} x$ 上，则 $y_{1}$ 与 $y_{2}$ 的关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、与m值有关

查看试题解析
8. 如图， $A B = A C$ ， $B C = B D = E D = E A$ ，则下列与 $∠ A$ 的度数最接近是（）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $36 °$

查看试题解析
9. 如图，等腰 $R t △ A B C$ ， $A C = B C$ ， $∠ C = 90 °$ ，点P由点B开始沿 $B C$ 边匀速运动到点C，再沿 $C A$ 边匀速运动到点A为止，设运动时间为t， $△ A B P$ 的面积为S，则S与t的大致图象是（）

A、 B、 C、 D、

查看试题解析
10. 如图，等边 $△ A B C$ 和等腰 $△ A B D$ ， $A B = B D$ ，点E，F分别为边 $A B$ ， $A D$ 的中点，若 $△ A B D$ 的面积为16， $A D = 4$ ，点M是CE上的动点，则 $△ A M F$ 的周长的最小值为（）

A、6 B、8 C、9 D、10

查看试题解析

二、填空题

11. 函数 $y = \frac{1}{x - 1}$ 的自变量的取值范围是．

查看试题解析
12. 将直线 $y = - 2 x + 3$ 向下平移 $a$ 个单位后恰好经过原点，则a的值是．

查看试题解析
13. 如图，点D，E分别在线段 $A B ， A C$ 上， $C D$ 与 $B E$ 相交于O点，已知 $A B = A C$ ，添加一个条件能直接用“ $A A S$ ”判定 $△ A B E ≌ △ A C D$ ，符合要求的条件是．

查看试题解析
14. 在 $△ A B C$ 中，已知 $∠ A = 60 °$ ， $∠ A B C$ 的平分线 $B D$ 与 $∠ A C B$ 的平分线 $C E$ 相交于点O， $∠ B O C$ 的平分线交 $B C$ 于F，则：

(1)、 $∠ B O E$ 的度数是．

(2)、若 $A B + A C = 15$ ， $A D + A E = 6$ ，则 $B C$ 的长是．

查看试题解析

三、解答题

15. 已知一次函数 $y = k x + b$ 的图象经过点 $A (- 2 ， - 3)$ 、点 $B (1 ， 6)$ ，求此一次函数的表达式．

查看试题解析
16. 在等腰 $△ A B C$ 中， $A B = 8$ ， $B C = 2 m + 2$ ， $A C = 20$ ，求m的值．

查看试题解析
17. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形） $A B C$ 的顶点A，C的坐标分别为 $A (2 ， 1)$ ， $C (- 1 ， 3)$ ．

(1)、请在如图所示的网格内作出x轴、y轴，并写出点B的坐标；

(2)、请作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，并直接写出 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
18. 在直角坐标系内，已知直线 $y = a x + b$ ，请画出直线 $2 x + y = 5$ ，并由图象解答：

(1)、写出方程组 ${\begin{array}{l} 2 x + y = 5 \\ y = a x + b \end{array}$ 的解；

(2)、写出不等式 $a x + b > - 2 x + 5$ 的解集．

查看试题解析
19. 某段时间内，汽车离开甲地到达乙地，并返回甲地，折线 $A B C D E$ 描述了汽车的行驶过程中汽车离甲地的路程s（千米）和行驶时间t（小时）之间的关系，根据图中提供的信息，解答下列问题：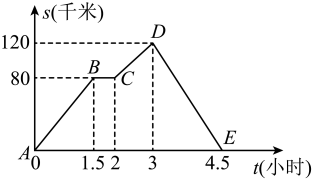

(1)、甲地与乙地之间的路程是千米，汽车在行驶途中停留了小时；

(2)、汽车在行驶过程中，哪段时间行驶速度最慢：（填“ $A B$ 段”“ $C D$ 段”或“ $D E$ 段”），此段时间共行驶千米；

(3)、汽车在返回时的平均速度是多少？

查看试题解析
20. 如图，E是 $△ A B C$ 内一点，AE的延长线交BC于D，连接EB，EC，且 $E B = E C$ ．

(1)、若 $∠ A B E = ∠ A C E$ ，求证： $A B = A C$ ；

(2)、若 $∠ B A E = ∠ C A E$ ，求证：AD垂直平分线段BC．

查看试题解析
21. 某农业科研单位，研究新型农作物的生长情况，发现试验田里的农作物每天的需水量y（千克）与生长时间x（天）之间的关系如折线图所示，这些农作物在第10天的需水量为2000千克，前40天中每天需水量比前一天增加50千克，在第40天后y与x的关系式为 $y = 100 x + m$ ．

(1)、第40天时，这些农作物的需水量是多少千克？并求出m的值；

(2)、若这些农作物每天的需水量大于4000千克时，需要进行人工灌溉增加水量，那么应从第几天开始进行人工灌溉？

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，且 $A C = B C$ ， D是 $A B$ 的中点，E是 $A B$ 延长线上一点， $A F ⊥ E C$ 交 $E C$ 的延长线于F， $A F$ 的延长线交 $D C$ 的延长线于点G，连接 $G E$ ．

(1)、求证：① $∠ A C G = ∠ C B E$ ；② $△ A C G ≌ △ C B E$ ；

(2)、若 $∠ G A E = 60 °$ ，求 $∠ C E G$ 的度数．

查看试题解析
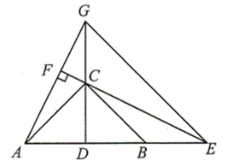23. 某班级社会实践小组组织“义卖活动”，计划从批发店购进甲、乙两类益智拼图，已知甲类拼图每盒进价比乙类拼图多5元，若购进甲类拼图20盒，乙类拼图30盒，则费用为600元．

(1)、求甲、乙两类拼图的每盒进价分别是多少元？

(2)、甲、乙两类拼图每盒售价分别为25元和18元．该班计划购进这两类拼图总费用不低于2100元且不超过2200元．若购进的甲、乙两类拼图共200盒，且全部售出，则甲类拼图为多少盒时，所获得总利润最大？最大利润为多少元？

(3)、在（2）的条件下，若该班级在“义卖活动”中，对售出的每一盒甲类拼图优惠 $a (0 < a \leq 5)$ 元，其他条件不变，则甲类拼图为多少盒时，所获得总利润最大，最大利润为多少元？（可用含a的式子表示）

查看试题解析