浙江省金华市金东区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、选择题(本大题有10小题,每小题3分,共30分.)
-
1. 下列事件中,是不可能事件的是( )A、买一张电影票,座位号是奇数 B、度量某个三角形的内角和,度数为185° C、打开电视机,正在播放新闻 D、射击运动员射击一次,命中9环2. 如图是一个由5个相同的正方体组成的立体图形,其俯视图是( )
 A、
A、 B、
B、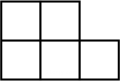 C、
C、 D、
D、 3. 抛物线的对称轴是直线( )A、 B、 C、 D、4. 如图,若的半径为6,圆心O到一条直线的距离为3,则这条直线可能是( )
3. 抛物线的对称轴是直线( )A、 B、 C、 D、4. 如图,若的半径为6,圆心O到一条直线的距离为3,则这条直线可能是( ) A、 B、 C、 D、5. 若 , 则( )A、 B、 C、 D、6. 如图,在中半径OC与弦AB垂直于点D,且 , 则CD的长为( )
A、 B、 C、 D、5. 若 , 则( )A、 B、 C、 D、6. 如图,在中半径OC与弦AB垂直于点D,且 , 则CD的长为( ) A、1 B、2 C、2.5 D、37. 如图,在中,已知点D,E分别是边AC,BC上的点, , 且 , 则等于( )
A、1 B、2 C、2.5 D、37. 如图,在中,已知点D,E分别是边AC,BC上的点, , 且 , 则等于( ) A、5:8 B、3:8 C、3:5 D、2:58. 已知是抛物线上的三点,则由小到大依序排列是( )A、 B、 C、 D、9. 如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
A、5:8 B、3:8 C、3:5 D、2:58. 已知是抛物线上的三点,则由小到大依序排列是( )A、 B、 C、 D、9. 如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( ) A、7 B、8 C、9 D、1610. 如图,的顶点是正方形网格的格点,则的值为( )
A、7 B、8 C、9 D、1610. 如图,的顶点是正方形网格的格点,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 如图,点A在x轴的正半轴上,点B坐标为 , 则值是 .
 12. 如图,A,B,C为上三点,且 , 则的度数是 .
12. 如图,A,B,C为上三点,且 , 则的度数是 . 13. 经过点 , 则不等式的解集是 .14. 如图是一个高为3cm的圆柱,其底面周长为 , 则该圆柱的表面积为 .
13. 经过点 , 则不等式的解集是 .14. 如图是一个高为3cm的圆柱,其底面周长为 , 则该圆柱的表面积为 . 15. 如图,半径为2的经过菱形ABCD的三个顶点A,D,C,且与AB相切于点A,则菱形的边长为 .
15. 如图,半径为2的经过菱形ABCD的三个顶点A,D,C,且与AB相切于点A,则菱形的边长为 . 16. 某古村落为方便游客泊车,准备利用长方形晒谷场长60m一侧,规划一个停车场,已知每个停车位需确保有如长5.5m,宽2.5m的长方形AEDF供停车,如图是其中一个停车位,所有停车位都平行排列,为60°,则每个体车位的面积大约为(结果保留整数),这个晒谷场按规划最多可容纳个停车位.()
16. 某古村落为方便游客泊车,准备利用长方形晒谷场长60m一侧,规划一个停车场,已知每个停车位需确保有如长5.5m,宽2.5m的长方形AEDF供停车,如图是其中一个停车位,所有停车位都平行排列,为60°,则每个体车位的面积大约为(结果保留整数),这个晒谷场按规划最多可容纳个停车位.()
三、解答题(本大题有8小题,共66分)
-
17. 计算:18. 某单位工会组织内部抽奖活动,共准备了100张奖券,设特等奖1个,一等奖10个,二等奖20个,三等奖30个.已知每张奖券获奖的可能性相同.求:(1)、一张奖券中特等奖的瓶率.(2)、一张奖券中奖的概率.(3)、一张奖券中一等奖或二等奖的概率.19. 已知抛物线经过点和点 ,(1)、求这个抛物线的解析式及顶点坐标.(2)、求抛物线与x轴两个交点之间的距离.20. 如图,在矩形ABCD中, , 动点E在边BC上,连结DE,过点A作 , 垂足为H,AH交CD于F.
 (1)、求证:;(2)、当时,求EC的长.21. 如图,AB是的直径,BC与相切,切点为B,AC与相交于点D,点E是上任一点.
(1)、求证:;(2)、当时,求EC的长.21. 如图,AB是的直径,BC与相切,切点为B,AC与相交于点D,点E是上任一点. (1)、求证: .(2)、已知 , 求阴影部分的面积.(结果保留)22. 如图,在中, , 点M是AC上一点,以CM为直径作 , AB与相切于点D,过点D作于点F,DE交于点E,连结CD,CE.
(1)、求证: .(2)、已知 , 求阴影部分的面积.(结果保留)22. 如图,在中, , 点M是AC上一点,以CM为直径作 , AB与相切于点D,过点D作于点F,DE交于点E,连结CD,CE. (1)、求证: .(2)、若 , 求CD的长.23. 记函数的图象为 , 函数的图象记为 , 图象和记为图象G.(1)、若点在图象G上,求m的值.(2)、已知直线l与x轴平行,且与图象G有三个交点,从左至右依次为点A,点B,点C,若 , 求点C坐标.(3)、若当时, , 求n的取值范围;24. 在矩形ABCD中, , 动点P从A出发,以1个单位每秒速度,沿射线AB方向运动,同时,动点Q从点C出发,以2个单位每秒速度,沿射线BC方向运动,设运动时间为t秒,连结DP,DQ.
(1)、求证: .(2)、若 , 求CD的长.23. 记函数的图象为 , 函数的图象记为 , 图象和记为图象G.(1)、若点在图象G上,求m的值.(2)、已知直线l与x轴平行,且与图象G有三个交点,从左至右依次为点A,点B,点C,若 , 求点C坐标.(3)、若当时, , 求n的取值范围;24. 在矩形ABCD中, , 动点P从A出发,以1个单位每秒速度,沿射线AB方向运动,同时,动点Q从点C出发,以2个单位每秒速度,沿射线BC方向运动,设运动时间为t秒,连结DP,DQ. (1)、如图1.证明: .(2)、作平分线交直线BC于点E;
(1)、如图1.证明: .(2)、作平分线交直线BC于点E;①图2,当点E与点B重合时,求t的值.
②连结PE,PQ,当与相似时,求t的值.