浙江省台州市温岭市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、选择题(本题有10小题,每小题4分,共40分.)
-
1. 2022年新能源车企迎来了更多的关注,如图是四款新能源汽车的标志,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列不是一元二次方程的是( )A、 B、 C、 D、3. 如果反比例函数的图象分布在第一、三象限,那么a的值可以是( )A、-3 B、2 C、0 D、-24. 下列事件中,属于必然事件的是( )A、明天会下雨 B、任意画一个三角形,其内角和为 C、抛一枚硬币,正面朝上 D、打开电视机,正在播放广告5. 如图,在平面直角坐标系中,将点A(3,2)绕原点O逆时针旋转90°得到点B,则点B的坐标为( )
2. 下列不是一元二次方程的是( )A、 B、 C、 D、3. 如果反比例函数的图象分布在第一、三象限,那么a的值可以是( )A、-3 B、2 C、0 D、-24. 下列事件中,属于必然事件的是( )A、明天会下雨 B、任意画一个三角形,其内角和为 C、抛一枚硬币,正面朝上 D、打开电视机,正在播放广告5. 如图,在平面直角坐标系中,将点A(3,2)绕原点O逆时针旋转90°得到点B,则点B的坐标为( ) A、(-2,3) B、(-3,2) C、(-2,-3) D、(-1,3)6. 二次函数与x轴交于(1,0)、(-3,0),则关于x的方程的解为( )A、1,3 B、1,-5 C、-1,3 D、1,-37. 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了x个人,下列所列方程正确的是( )A、 B、 C、 D、8. 如图,已知点A、点C在⊙O上,AB是⊙O切线,连接AC,若∠ACO=65°,则∠CAB的度数为( )
A、(-2,3) B、(-3,2) C、(-2,-3) D、(-1,3)6. 二次函数与x轴交于(1,0)、(-3,0),则关于x的方程的解为( )A、1,3 B、1,-5 C、-1,3 D、1,-37. 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了x个人,下列所列方程正确的是( )A、 B、 C、 D、8. 如图,已知点A、点C在⊙O上,AB是⊙O切线,连接AC,若∠ACO=65°,则∠CAB的度数为( ) A、35° B、30° C、25° D、20°9. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )
A、35° B、30° C、25° D、20°9. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )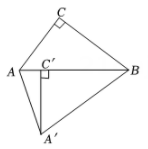 A、 B、4 C、 D、510. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
A、 B、4 C、 D、510. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则二、填空题(本题有6小题,每小题5分,共30分).
-
11. 点关于原点对称的点的坐标为 .12. 某射击运动员封闭训练10个月,每天击中9环以上的频率记录如下图,封闭训练结束时,估计这名运动员射击一次时“击中9环以上”的概率为(结果保留一位小数).
 13. 关于的方程没有实数根,则的取值范围为 .14. 如图,已知与是公路弯道的外、内边线,它们有共同的圆心 , 所对的圆心角都是、A、C、O在同一直线上,公路宽米,则弯道外侧边线比内侧边线多米(结果保留).
13. 关于的方程没有实数根,则的取值范围为 .14. 如图,已知与是公路弯道的外、内边线,它们有共同的圆心 , 所对的圆心角都是、A、C、O在同一直线上,公路宽米,则弯道外侧边线比内侧边线多米(结果保留). 15. 关于的二次函数 , 在时有最大值6,则 .16. 如图,把双曲线绕着原点逆时针旋转与轴交于点 ,
15. 关于的二次函数 , 在时有最大值6,则 .16. 如图,把双曲线绕着原点逆时针旋转与轴交于点 , (1)、若点B(0,2),则k=;(2)、若点A(3,5)在旋转后的曲线上,则k= .
(1)、若点B(0,2),则k=;(2)、若点A(3,5)在旋转后的曲线上,则k= .三、解答题(第17~20题,每题8分,第21题10分,第22-23题,每题12分,第24题14分,共80分)
-
17. 解方程: .18. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
 (1)、求这个反比例函数的解析式,并直接写出蓄电池的电压值(单位:v)(2)、如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?19. 象棋比赛中,采用翻扑克牌比大小的方式决定哪方先走子,五张扑克牌点数分别是1、2、3、4、5,背面无差别,将扑克牌背面朝上,由参赛棋手中一方先翻出一张,然后另一方翻剩下的四张中的一张,点数大者先走;(1)、棋手甲先翻出点数是4,甲先走的概率是;(2)、两轮比赛,假设棋手甲翻出点数都是3,求两轮都是甲先走的概率(用画树状图或列表的方法求解)。20. 如图,已知一抛物线形大门,其地面宽度为10m,一身高为1.8m的同学站在门内,在离门脚1m处垂直地面站直拍照,其头顶恰好顶在抛物线形门上,根据这些条件,请你求出该大门的高h.
(1)、求这个反比例函数的解析式,并直接写出蓄电池的电压值(单位:v)(2)、如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?19. 象棋比赛中,采用翻扑克牌比大小的方式决定哪方先走子,五张扑克牌点数分别是1、2、3、4、5,背面无差别,将扑克牌背面朝上,由参赛棋手中一方先翻出一张,然后另一方翻剩下的四张中的一张,点数大者先走;(1)、棋手甲先翻出点数是4,甲先走的概率是;(2)、两轮比赛,假设棋手甲翻出点数都是3,求两轮都是甲先走的概率(用画树状图或列表的方法求解)。20. 如图,已知一抛物线形大门,其地面宽度为10m,一身高为1.8m的同学站在门内,在离门脚1m处垂直地面站直拍照,其头顶恰好顶在抛物线形门上,根据这些条件,请你求出该大门的高h. 21. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑)
21. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑) (1)、如图1,判断圆心O▲ (填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;22. 如图,将△ABC绕点A顺时针旋转得到△AED,并使C点的对应点D点落在直线BC上,
(1)、如图1,判断圆心O▲ (填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;22. 如图,将△ABC绕点A顺时针旋转得到△AED,并使C点的对应点D点落在直线BC上,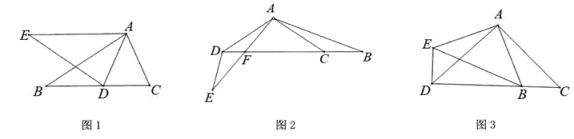 (1)、如图1,证明:DA平分∠EDC;(2)、如图2,AE与BD交于点F,若∠AFB=50°,∠B=20°,求∠BAC的度数;(3)、如图3,连接BE,若EB=13,ED=5,CD=17,则AD的长为 .23. 如图1,小球从倾斜轨道AB由静止滚下时,经过的路程s(米)与时间t(秒)的部分数据如下表.
(1)、如图1,证明:DA平分∠EDC;(2)、如图2,AE与BD交于点F,若∠AFB=50°,∠B=20°,求∠BAC的度数;(3)、如图3,连接BE,若EB=13,ED=5,CD=17,则AD的长为 .23. 如图1,小球从倾斜轨道AB由静止滚下时,经过的路程s(米)与时间t(秒)的部分数据如下表.t(秒)
0
0.4
0.8
1
1.2
1.6
…
s(米)
0
0.016
0.064
0.1
0.144
0.256
…
 (1)、请在一次函数、二次函数、反比例函数中选择最适合s与t的函数类型,并求出解析式;(2)、经过多少秒时,路程为0.225米?(3)、如图2,与轨道AB相连的是一段水平光滑轨道BC,BC的另一端连接的是与AB平行的轨道CD,CD足够长。两个同样的小球甲与乙分别从A、C处同时静止滚下,其中甲球在BC上滚动的时间是2秒,速度是0.4米/秒,问总运动时间为多少时,两球滚过的路程差为1.6米?
(1)、请在一次函数、二次函数、反比例函数中选择最适合s与t的函数类型,并求出解析式;(2)、经过多少秒时,路程为0.225米?(3)、如图2,与轨道AB相连的是一段水平光滑轨道BC,BC的另一端连接的是与AB平行的轨道CD,CD足够长。两个同样的小球甲与乙分别从A、C处同时静止滚下,其中甲球在BC上滚动的时间是2秒,速度是0.4米/秒,问总运动时间为多少时,两球滚过的路程差为1.6米?(注:小球大小忽略不计,小球在下一段轨道的开始速度等于它在上一段轨道的最后速度)
24. 如图⊙O半径为r,锐角△ABC内接于⊙O,连AO并延长交BC于D,过点D作DE⊥AC于E. (1)、如图1,求证:∠DAB=∠CDE;(2)、如图1,若CD=OA,AB=6,求DE的长;(3)、如图2,当∠DAC=2∠DAB时,BD=5,DC=6,求r的值;(4)、如图3,若AE=AB=BD=1,直接写出AD+DE的值(用含r的代数式表示)
(1)、如图1,求证:∠DAB=∠CDE;(2)、如图1,若CD=OA,AB=6,求DE的长;(3)、如图2,当∠DAC=2∠DAB时,BD=5,DC=6,求r的值;(4)、如图3,若AE=AB=BD=1,直接写出AD+DE的值(用含r的代数式表示)