四川省成都市高新区2022-2023学年九年级上学期数学期末试题
试卷更新日期:2023-02-01 类型:期末考试
一、选择题(本大题共8小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
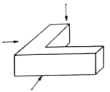
1. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、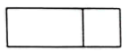 D、
D、 2. 如图,点P在的边AC上,要判断 , 添加下列一个条件,不正确的是( )
2. 如图,点P在的边AC上,要判断 , 添加下列一个条件,不正确的是( ) A、 B、 C、 D、3. 已知反比例函数的图象经过点 , 那么下列四个点中,也在这个函数图象上的是( )A、 B、 C、 D、4. 一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在左右,则袋子中的黄球个数最有可能是( )A、1 B、2 C、4 D、65. 如图,矩形ABCD∽矩形EFGH,已知 , , , 则FG的长为( )
A、 B、 C、 D、3. 已知反比例函数的图象经过点 , 那么下列四个点中,也在这个函数图象上的是( )A、 B、 C、 D、4. 一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在左右,则袋子中的黄球个数最有可能是( )A、1 B、2 C、4 D、65. 如图,矩形ABCD∽矩形EFGH,已知 , , , 则FG的长为( )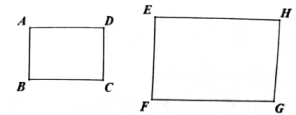 A、8cm B、10cm C、12cm D、15cm6. 如图,在中, , 点D为边AB的中点, , , 则BC的长为( )
A、8cm B、10cm C、12cm D、15cm6. 如图,在中, , 点D为边AB的中点, , , 则BC的长为( ) A、3 B、4 C、6 D、7. 两个相似三角形一组对应角平分线的长分别是2cm和5cm,其中较小三角形的周长是10cm,则较大三角形的周长为( )A、15cm B、18cm C、20cm D、25cm8. 某公司前年缴税40万元,今年缴税48.4万元,求该公司这两年缴税的年平均增长率为多少.设该公司这两年缴税的年平均增长率为x,根据题意,下列所列的方程正确的是( )A、 B、 C、 D、
A、3 B、4 C、6 D、7. 两个相似三角形一组对应角平分线的长分别是2cm和5cm,其中较小三角形的周长是10cm,则较大三角形的周长为( )A、15cm B、18cm C、20cm D、25cm8. 某公司前年缴税40万元,今年缴税48.4万元,求该公司这两年缴税的年平均增长率为多少.设该公司这两年缴税的年平均增长率为x,根据题意,下列所列的方程正确的是( )A、 B、 C、 D、二、填空题(本大题共5个小题,每小题4分,共20分,)
-
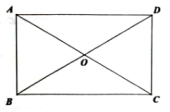
9. 已知 , 则的值= .10. 如图,在矩形ABCD中,对角线AC,BD交于点O,若 , 则 .
 11. 已知点与点都在反比例函数的图象上,且 , 那么(填“>”,“=”或“<”).12. 已知两条直线被三条平行线所截,截得线段的长度如图所示,则 .
11. 已知点与点都在反比例函数的图象上,且 , 那么(填“>”,“=”或“<”).12. 已知两条直线被三条平行线所截,截得线段的长度如图所示,则 .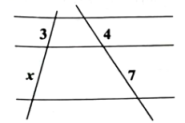 13. 如图,平面直角坐标系中,一点光源位于 , 线段BC的两个端点坐标分别为与 , 则线段BC在x轴上的影子的长度为 .
13. 如图,平面直角坐标系中,一点光源位于 , 线段BC的两个端点坐标分别为与 , 则线段BC在x轴上的影子的长度为 .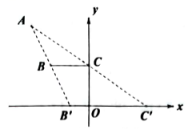
三、解答题(本大题共5个小题,共48分)
-
14.(1)、解方程;(2)、关于x的一元二次方程有两个相等的实数根,求m的值.15. 某校同学参与“项目式学习”综合实践活动,小明所在的数学活动小组利用所学知识测量旗杆EF的高度,他在距离旗杆40米的D处立下一根3米高的竖直标杆CD,然后调整自己的位置,当他与标杆的距离BD为4米时,他的眼睛、标杆顶端和旗杆顶位于同一直线上,若小明的眼睛离地面高度AB为1.6米,求旗杆EF的高度.
 16. 为深入推进“双减”,促进优质教育资源共享,更好地满足学生学习发展的需求,成都市教育局推出了“名师导学+在线答疑”服务,为有需求的学生答疑解惑.某学校为了解学生对该服务的了解情况,随机抽取若干名九年级学生进行调查,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解.”四种,并将调查结果绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
16. 为深入推进“双减”,促进优质教育资源共享,更好地满足学生学习发展的需求,成都市教育局推出了“名师导学+在线答疑”服务,为有需求的学生答疑解惑.某学校为了解学生对该服务的了解情况,随机抽取若干名九年级学生进行调查,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解.”四种,并将调查结果绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: (1)、 ▲ , 并补全条形统计图;(2)、若该校九年级学生人数为500名,根据调查结果,估计该校对“名师导学+在线答疑”服务“比较了解”的学生共有名;(3)、已知对“名师导学+在线答疑”服务“非常了解”的是1名男生和3名女生,从中随机抽取2名向其他同学做介绍,请用画树状图或列表的方法,求恰好抽到1男1女的概率.17. 矩形ABCD中,连接AC,∠CAD的平分线交CD于点E,交BC的延长线于点F,在线段EF上取点G,使 .
(1)、 ▲ , 并补全条形统计图;(2)、若该校九年级学生人数为500名,根据调查结果,估计该校对“名师导学+在线答疑”服务“比较了解”的学生共有名;(3)、已知对“名师导学+在线答疑”服务“非常了解”的是1名男生和3名女生,从中随机抽取2名向其他同学做介绍,请用画树状图或列表的方法,求恰好抽到1男1女的概率.17. 矩形ABCD中,连接AC,∠CAD的平分线交CD于点E,交BC的延长线于点F,在线段EF上取点G,使 .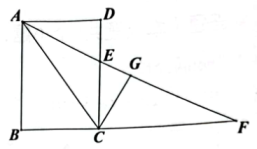 (1)、判断三角形ACF的形状,并证明;(2)、若 , , 求CE及CG的长.18. 如图,平面直角坐标系中,过点的直线与反比例函数的图象交于点A.
(1)、判断三角形ACF的形状,并证明;(2)、若 , , 求CE及CG的长.18. 如图,平面直角坐标系中,过点的直线与反比例函数的图象交于点A.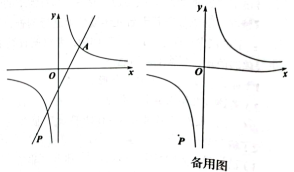 (1)、若点A的横坐标1,求直线AP的函数表达式;(2)、在(1)的条件下,点B为第一象限的反比例函数图象上一点,且在直线PA上方,若 , 求点B的坐标;(3)、过点P的另一条直线与反比例函数的图象交于M,N两点,点M在第一象限,若 , 求点N的坐标.
(1)、若点A的横坐标1,求直线AP的函数表达式;(2)、在(1)的条件下,点B为第一象限的反比例函数图象上一点,且在直线PA上方,若 , 求点B的坐标;(3)、过点P的另一条直线与反比例函数的图象交于M,N两点,点M在第一象限,若 , 求点N的坐标.四、B卷-填空题(本大题共5个小题,每小题4分,共20分)
-
19. 若m,n是一元二次方程的两实根,则的值为 .20. 用如图所示的两个转盘进行“配紫色”游戏,则配得紫色的概率是 . (若其中一个转盘转出蓝色,另一个转盘转出红色,则配得紫色)
 21. 黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为cm.(结果保留根号)
21. 黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为cm.(结果保留根号) 22. 如图,在平面直角坐标中,平行四边形ABCD顶点A的坐标为 , 点D在反比例函数的图象上,点B,C在反比例函数的图象上,CD与y轴交于点E,若 , , 则k的值为 .
22. 如图,在平面直角坐标中,平行四边形ABCD顶点A的坐标为 , 点D在反比例函数的图象上,点B,C在反比例函数的图象上,CD与y轴交于点E,若 , , 则k的值为 . 23. 如图,中, , , 点E为AC中点.点D在AC右侧, , 且 , 射线BE交AD于点F,若为等腰三角形,则线段EF的长为 .
23. 如图,中, , , 点E为AC中点.点D在AC右侧, , 且 , 射线BE交AD于点F,若为等腰三角形,则线段EF的长为 .
五、B卷-解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
24. 如图,某校准备用54米的围栏修建一边靠墙的矩形花园 , 已知墙体的最大可用长度为28米,设AB的长为x米,矩形花园的面积为y平方米.
 (1)、请用含有x的代数式表示y,并写出自变量x的取值范围;(2)、如果该矩形花园的面积为360平方米,求AB的长.25. 已知直线:分别与x轴,y轴交于A,B两点,直线:与y轴交于点C,与直线交于点D.点P是线段OA上一动点(不与O,A重合),连接CP.
(1)、请用含有x的代数式表示y,并写出自变量x的取值范围;(2)、如果该矩形花园的面积为360平方米,求AB的长.25. 已知直线:分别与x轴,y轴交于A,B两点,直线:与y轴交于点C,与直线交于点D.点P是线段OA上一动点(不与O,A重合),连接CP.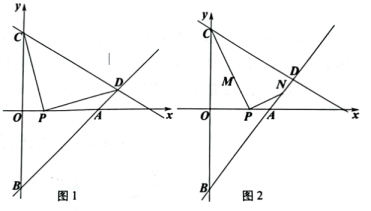 (1)、如图1,点D的横坐标为5.
(1)、如图1,点D的横坐标为5.i)求直线的函数表达式;
ii)连接DP,若 , 求线段OP的长;
(2)、如图2,若 , 在线段CP上取点M,将线段MP绕点P顺时针旋转90°得到PN,点N恰好在直线上,且 , 求线段PM的长.26. 如图1,在中,对角线AC,BD交于点O,AC平分∠BAD. (1)、求证:四边形ABCD为菱形;(2)、如图2,已知四边形ABCD的面积为20, , 点E在BC的延长线上,点F在AD的延长线上,连接EF.
(1)、求证:四边形ABCD为菱形;(2)、如图2,已知四边形ABCD的面积为20, , 点E在BC的延长线上,点F在AD的延长线上,连接EF.i)若 , 连接OE,OF,求线段OF的长及的面积;
ii)过点C作AC的垂线交EF的延长线于点M,连接AM,点P为AM的中点,若四边形CFMP为菱形,求线段CE的长.