四川省达州市通川八中2022-2023学年八年级上学期期末数学试卷
试卷更新日期:2023-02-01 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 在-1.414, , π,2+ , 3.212212221…,3.14这些数中,无理数的个数为( )A、5 B、2 C、3 D、42. 以下列各组数中的三个数据为边长构建三角形,能组成直角三角形的一组是( )
A、7,14,15 B、12,16,20 C、4,6,8 D、 , ,3. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、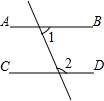 B、
B、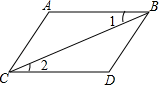 C、
C、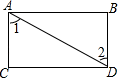 D、
D、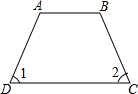 4. 每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
4. 每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:册数
0
1
2
3
4
人数
3
13
16
17
1
则这50名学生读书册数的众数、中位数是( )
A、3,3 B、3,2 C、2,3 D、2,25. 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( ) A、m=n B、m>n C、m<n D、m、n的大小关系不确定6. 已知是二元一次方程组的解,则2m-n的算术平方根为( )A、±2 B、 C、2 D、47. 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
A、m=n B、m>n C、m<n D、m、n的大小关系不确定6. 已知是二元一次方程组的解,则2m-n的算术平方根为( )A、±2 B、 C、2 D、47. 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( ) A、110° B、120° C、130° D、140°8. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标( )
A、110° B、120° C、130° D、140°8. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标( ) A、(4,10) B、(10,6) C、(10,4) D、(10,3)9. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,设用x张制盒身,y张制盒底,恰好配套制成罐头盒.则下列方程组中符合题意的是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )
A、(4,10) B、(10,6) C、(10,4) D、(10,3)9. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,设用x张制盒身,y张制盒底,恰好配套制成罐头盒.则下列方程组中符合题意的是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( ) A、-2 B、1 C、 D、2
A、-2 B、1 C、 D、2二、填空题(每小题3分,共18分)
-
11. 在2015年的体育考试中某校6名学生的体育成绩统计如图所示,这组数据的中位数是 .
 12. 如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
12. 如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= . 13. 函数y=kx+b(k≠0)的图象平行于直线y=2x+3,且交y轴于点(0,-1),则其解析式是 .14. 已知直线x+2y=5与直线x+y=3的交点坐标是(1,2),则方程组的解是 .15. 如图,把一副三角板的两个直角三角形叠放在一起,则α的度数为 .
13. 函数y=kx+b(k≠0)的图象平行于直线y=2x+3,且交y轴于点(0,-1),则其解析式是 .14. 已知直线x+2y=5与直线x+y=3的交点坐标是(1,2),则方程组的解是 .15. 如图,把一副三角板的两个直角三角形叠放在一起,则α的度数为 . 16. 如图,长方体的底面边长分别为 和 ,高为 .若一只蚂蚁从 点开始经过 个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径长为 .
16. 如图,长方体的底面边长分别为 和 ,高为 .若一只蚂蚁从 点开始经过 个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径长为 .
三、解答题(共72分)
-
17. 计算:(1)、(-)(+)+;(2)、 .18. 解下列方程组(1)、(2)、 .19. 如图,△ABC是正方形网格上的格点三角形(顶点A、B、C在正方形网格的格点上)

⑴画出△ABC关于直线l的对称图形;
⑵画出以P为顶点且与△ABC全等的格点三角形.(规定:点P与点B对应)
20. 已知:如图,直线BD分别交射线AE、CF于点B、D,连接A、D和B、C,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证: (1)、AD∥BC;(2)、BC平分∠DBE.21. 开展“创卫”活动,某校倡议学生利用双休日在“人民公园”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)、AD∥BC;(2)、BC平分∠DBE.21. 开展“创卫”活动,某校倡议学生利用双休日在“人民公园”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
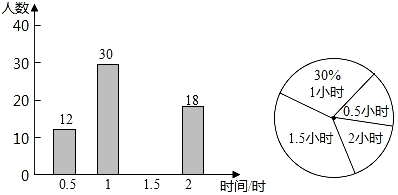 (1)、将条形统计图补充完整;(2)、求抽查的学生劳动时间的众数、中位数;(3)、电视台要从参加义务劳动的学生中随机抽取1名同学采访,抽到时参加义务劳动的时间为2小时的同学概率是多少?22. 我市为加快美丽乡村建设,建设秀美幸福抚州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.(1)、建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?(2)、乙镇3个A类美丽村庄和4个B类村庄改建共需资金多少万元?23. 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
(1)、将条形统计图补充完整;(2)、求抽查的学生劳动时间的众数、中位数;(3)、电视台要从参加义务劳动的学生中随机抽取1名同学采访,抽到时参加义务劳动的时间为2小时的同学概率是多少?22. 我市为加快美丽乡村建设,建设秀美幸福抚州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.(1)、建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?(2)、乙镇3个A类美丽村庄和4个B类村庄改建共需资金多少万元?23. 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M. (1)、求证:△ADC≌△AEB;(2)、判断△EGM是什么三角形,并证明你的结论;(3)、判断线段BG、AF与FG的数量关系并证明你的结论.24. 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)、求证:△ADC≌△AEB;(2)、判断△EGM是什么三角形,并证明你的结论;(3)、判断线段BG、AF与FG的数量关系并证明你的结论.24. 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC. (1)、填空:点A的坐标:;点B的坐标: .(2)、若CD平分∠ACO,交x轴于D,求点D的坐标.(3)、在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求该直线的解析式.25. 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.
(1)、填空:点A的坐标:;点B的坐标: .(2)、若CD平分∠ACO,交x轴于D,求点D的坐标.(3)、在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求该直线的解析式.25. 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C. (1)、求点D的坐标;(2)、求直线l2的解析表达式;(3)、求△ADC的面积;(4)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
(1)、求点D的坐标;(2)、求直线l2的解析表达式;(3)、求△ADC的面积;(4)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.