浙江省杭州市拱墅区锦绣育才教育集团2022-2023学年七年级上学期期末数学试卷

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 中国古代数学著作《九章数学》的“方程”一章，在世界数学史上首次正式引入负数，如果收入100元记作+100元，那么-75元表示（）

A、支出-75元 B、收入75元 C、支出75元 D、收入25元

查看试题解析
2. 2022年十三届全国人大五次会议审议通过的政府工作报告中提出，今年城镇新增就业目标为11000000人以上.数据11000000用科学记数法表示正确的是（）

A、 0.11×10⁷ B、1.1×10⁷ C、1.1×10⁶ D、11×10⁶

查看试题解析
3. 下列说法正确的是（）

A、4的平方根是2 B、8的立方根是±2 C、 $\sqrt{{(- 3)}^{2}}$ ＝-3 D、-6没有平方根

查看试题解析
4. 单项式x^m+3y²与-4xyⁿ是同类项，则mn的值是（）

A、4 B、-4 C、6 D、-6

查看试题解析
5. 下列说法中，正确的是（）

A、两点之间直线最短 B、如果∠α＝53°38'，那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在，那么这个角的余角比这个角的补角小 D、相等的角是对顶角

查看试题解析
6. 若2a²+b＝4，则代数式3-4a²-2b的值为（）

A、11 B、7 C、-1 D、-5

查看试题解析
7. 如图，面积为5的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则E点所表示的数为（）

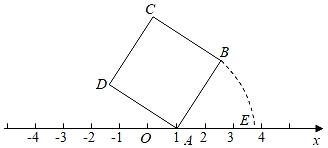A、 $\sqrt{5}$ B、1+ $\sqrt{5}$ C、 $\frac{2 + \sqrt{5}}{2}$ D、 $\sqrt{5}$ +2

查看试题解析
8. 如图，点B，点C都在线段AD上，若AD＝2BC，则（）

A、AB＝CD B、AB+CD＝BC C、AC-CD＝BC D、AD+BC＝2AC

查看试题解析
9. 《孙子算经》是中国古代数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木头，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余一尺，问木头长多少尺？可设木头长为x尺，则所列方程正确的是（）

A、（x+4.5）-2x＝1 B、2x-（x+4.5）＝1 C、x- $\frac{x + 4.5}{2}$ ＝1 D、 $\frac{x + 4.5}{2}$ -x＝1

查看试题解析
10. 现有1张大长方形和3张相同的小长方形卡片，按如图所示两种方式摆放，则小长方形的长与宽的差是（）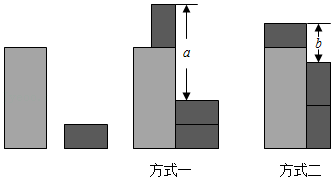

A、a-b B、 $\frac{a - b}{2}$ C、 $\frac{a - b}{3}$ D、 $\frac{a + b}{3}$

查看试题解析

二、填空题（每小题4分，共24分）

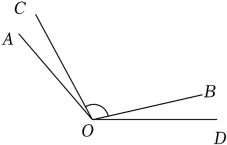
11. ﹣4的绝对值是．

查看试题解析
12. “m的2倍与n的差”用代数式表示为.

查看试题解析
13. 若x＝2是关于x的方程5x+a＝3（x+3）的解，则a的值是．

查看试题解析
14. 如图，∠AOB＝∠COD＝120°，若∠BOC＝108°，则∠AOD的度数是.

查看试题解析
15. 如图，已知线段AB＝8，延长BA至点C，使AC＝ $\frac{1}{2}$ AB，D为线段BC的中点，则AD＝.

查看试题解析
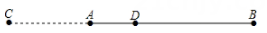16. 某水果店销售40千克香蕉，第一天售价为8元/千克，第二天降为6元/千克，第三天再降为4元/千克.三天全部售完，共计所得240元.若该店第二天销售香蕉k千克，则第三天销售香蕉千克.（用含k的代数式表示）

查看试题解析

三、解答题（共7道题，共66分）

17. 计算：

(1)、2+（-3）-（-5）；

(2)、（-3）²÷（- $\frac{3}{2}$ ）+ $\sqrt[3]{8}$ .

查看试题解析
18. 解方程：

(1)、5+2x＝4；

(2)、 $1 - \frac{4 - 3 x}{4} = \frac{5 x + 3}{6} - x$ .

查看试题解析
19. 如图，直线AB、CD相交于点O，OM⊥AB.

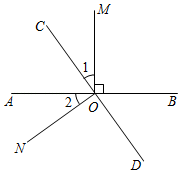(1)、若∠1＝∠2，证明：ON⊥CD；

(2)、若∠1＝ $\frac{1}{3}$ ∠BOC，求∠BOD的度数.

查看试题解析
20. 已知一个正数m的平方根为2n+1和4-3n.

(1)、求m的值；

(2)、|a-1|+ $\sqrt{b}$ +（c-n）²＝0，a+b+c的平方根是多少？

查看试题解析
21. 数学家欧拉最先把关于x的多项式用记号f（x）来表示.例如：f（x）＝x²+x-1，当x＝a时.多项式的值用f（a）来表示，即f（a）＝a²+a-1.当x＝3时，f（3）＝3²+3-1＝11.

(1)、已知f（x）＝x²-2x+3，求f（1）的值.

(2)、已知f（x）＝mx²-2x-m，当f（-3）＝m-1时，求m的值.

(3)、已知f（x）＝kx²-ax-bk（a.b为常数），对于任意有理数k，总有f（-2）＝-2，求a，b的值.

查看试题解析
22. 如图，已知数轴上点A表示的数为10，点B位于点A左侧，AB＝15．动点P从点A出发，以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．

(1)、当点P在A、B两点之间运动时，
①用含t的代数式表示PB的长度；

②若PB＝2PA，求点P所表示的数；

(2)、动点Q从点B出发，以每秒5个单位长度的速度沿数轴向右匀速运动，当点Q到达点A后立即原速返回．若P，Q两点同时出发，其中一点运动到点B时，两点停止运动．求在这个运动过程中，P，Q两点相遇时t的值．

查看试题解析

23. 一家电信公司推出手机话费套餐活动，具体资费标准见表；

套餐月租费（元/月）	套餐内容		套餐外资费
套餐月租费（元/月）	主叫限定时间（分钟）	被叫	主叫超时费（元/分钟）
58	50	免费	0.25
88	150		0.20
118	350		0.15
说明：①主叫：主动打电话给别人；被叫：接听别人打进来的电话. ②若办理的是月租费为58元的套餐，主叫时间不超过50分钟时，当月话费即为58元；若主叫时间为60分钟，则当月话费为58+0.25×（60-50）＝60.5元. 其它套餐计费方法类似.

(1)、已知小聪办理的是月租费为88元的套餐，小明办理的是月租费为118元的套餐.

①若他们某一月的主叫时间都为200分钟，分别计算两人的话费.

②若他们某一月的主叫时间都为m分钟（m＞360），请用含m的代数式分别表示该月他们的话费.

(2)、若小慧的两个手机号码分别办理了58元、88元套餐.该月她的两个号码主叫时间共为220分钟，总话费为152元，求她两个号的主叫时间分别可能是多少分钟.

查看试题解析