重庆市北碚区2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-02-01 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $a^{2 m + 1}$ 与 $3 {a^{m}}^{+ 2}$ 是同类项，则m等于（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下列方程：
① $2 x^{2} - x = 6$ ；② $y = x - 7$ ；③ $\frac{2}{3} m - 5 = m$ ；④ $\frac{2}{x - 1} = 1$ ；⑤ $\frac{x - 3}{2} = 1$ ；⑥ $x = 3$ ，
其中是一元一次方程的有（）

A、2个 B、3个 C、4个 D、以上答案都不对

查看试题解析
3. 如图，是正方体的展开图的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
5. 不等式组 $- 2 \leq x + 1 < 1$ 的解集，在数轴上表示正确的是（）

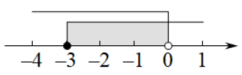A、 B、 C、 D、

查看试题解析
6. 下列说法正确的有（）个
①两点确定一条直线；②两点之间，直线最短；③角的两边越长，角就越大；④若线段 $A B = B C$ ，则点B是线段 $A C$ 的中点.

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 不等式组 ${\begin{array}{l} \frac{1}{2} x + 1 > - 3 \\ x - 2 (x - 3) > 0 \end{array}$ 的最小整数解为（）

A、 $- 8$ B、 $- 7$ C、 $- 6$ D、 $- 5$

查看试题解析
8. 某校运动员分组训练.若每组5人，余3人；若每组6人.则缺5人；设运动员人数为x人，组数为y组，则列方程组为（）

A、 ${\begin{array}{l} 5 y = x + 3 \\ 6 y + 5 = x \end{array}$ B、 ${\begin{array}{l} 5 y = x - 3 \\ 6 y + 5 = x \end{array}$ C、 ${\begin{array}{l} 5 y = x - 3 \\ 6 y = x + 5 \end{array}$ D、 ${\begin{array}{l} 5 y = x + 3 \\ 6 y = x + 5 \end{array}$

查看试题解析
9. ${\begin{array}{l} a - b + c = 0 \\ 2 a - 3 b + c = 0 \end{array}$ ，则 $\frac{a - c}{b} =$ （）

A、1 B、2 C、3 D、4

查看试题解析
10. 若不等式组 ${\begin{array}{l} x - 1 > a \\ x - 3 \leq 0 \end{array}$ 有解，则a的取值范围是（）

A、 $a \leq 3$ B、 $a < 3$ C、 $a < 2$ D、 $a \leq 2$

查看试题解析
11. 为安置50名培训人员入住，需要同时租用6人间和4人间两种客房，若每个房间都住满，则租房方案共有（）

A、4种 B、5种 C、6种 D、7种

查看试题解析
12. 若关于x的不等式组 ${\begin{array}{l} \frac{x + 5}{2} < x - 1 \\ 2 x + 2 < x + a \end{array}$ 只有4个整数解，则a的取值范围是（）

A、 $a \geq 13$ B、 $13 < a < 14$ C、 $13 \leq a < 14$ D、 $13 < a \leq 14$

查看试题解析

二、填空题

13. 当 $a =$ 时， $4 a - 5$ 与 $5 a - 4$ 的值互为相反数.

查看试题解析
14. 若关于x，y的二元一次方程组 ${\begin{array}{l} 3 x + y = 1 + a \\ x + 3 y = 3 \end{array}$ 的解满足 $x + y = 2$ .则 $a =$ .

查看试题解析
15. 时钟上 $6 ： 40$ 时针和分针的夹角是度.

查看试题解析
16. 重百十周年店庆，小明妈妈以平时八折的优惠购买了一件衣服，节省24元，那么小明妈妈购买这件衣服实际花费了元.

查看试题解析
17. 直线l上的线段 $A B 、 B C$ 分别长 $4 c m ， 8 c m$ ， M、N分别是 $A B ， B C$ 的中点，则 $M N =$ $c m$ .

查看试题解析
18. 要使方程组 ${\begin{array}{l} 2 x + a y = 8 \\ x - 2 y = 0 \end{array}$ 有正整数解，则整数a有个.

查看试题解析
19. 我们用 $< a >$ 表示不小于a的最小整数，例如： $< 2.5 > = 3$ ， $⟨ 4 ⟩ = 4$ ， $< - 1.5 > = - 1$ .若 $< \frac{x + 3}{2} > = 1$ ，则x的取值范围是.

查看试题解析
20. 沁园的一种饮品是由果汁原液和纯净水按一定比例配制而成，其中购买一吨果汁原液的钱可以购买18吨纯净水.由于今年果汁价格上 $30 %$ .纯净水价格也上涨了 $5 %$ ，导致配制的这种饮品价格上涨 $25 %$ ，问这种饮品果汁与纯净水的配制比例是.

查看试题解析

三、解答题

21. 解一元一次方程：

(1)、 $2 x + 3 = x + 8$ .

(2)、 $\frac{2 x - 1}{3} - \frac{5 x - 1}{6} = 1$ .

查看试题解析
22. 解二元一次方程组：

(1)、 ${\begin{array}{l} x + 3 y = 9 \\ x - y = 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 2 x - 3 y = 3 \\ 3 x + 2 y = 11 \end{array}$ .

查看试题解析
23. 解二元一次不等式（组）：

(1)、 $3 - 2 （ x - 4 ） > 3 x - 1$ .

(2)、 ${\begin{array}{l} 3 x + 1 < x - 3 \\ \frac{1 + x}{2} \leq \frac{1 + 2 x}{3} + 1 \end{array}$ .

查看试题解析
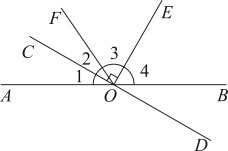24. 如图，已知直线 $A B$ 和 $C D$ 相交于点O， $∠ C O E$ 为直角， $O F$ 平分 $∠ A O E$ ， $∠ C O F = 28 °$ .求 $∠ B O E$ 的度数.

查看试题解析
25. 甲、乙两人同时从A地去B地，A、B两地相距12千米，甲骑自行车，乙步行，甲的速度比乙的速度的2倍还快2千米/时，甲到达B立刻返回在途中遇到乙，这时距他们出发时已过了3小时，求乙的速度.

查看试题解析
26. 永辉超市要购进A、B两种型号的电压力锅，已知购进2台A和3台B花费1650元；购进1台A和2台B花费1000元.

(1)、求A和B两种型号的压力锅每台进价分别是多少元.

(2)、为了满足市场需求，超市决定用不超过19150元采购A、B两种型号的压力锅共60台，且B型号压力锅的数量的2倍不低于A型号压力锅，该商场有几种进货方式.

(3)、在（2）的条件下A型号压力锅促销期间售价是389元，B型号压力锅促销期间售价是469元，该超市选择哪种进货方式利润最大.

查看试题解析
27. 对于一个三位数 $\begin{array}{l} n = a b c \end{array}$ ，如果满足 $a > b > c$ ，则称这个三位数n为“博雅数”.将一个博雅数“百位与十位的差、百位与个位的差、十位与个位的差的和与3的商记为 $F (n)$ .例如n=521，则：F（521）= $\frac{(5 - 2) + (5 - 1) + (2 - 1)}{3} = \frac{3 + 4 + 1}{3} = \frac{8}{3}$ .

(1)、计算： $F (841) ， F (532)$ .

(2)、若s，t堤博雅数”，其中. $s = 970 + x ， t = 100 y + 32 (0 \leq x \leq 9 ， 1 \leq y \leq 9 ， x ， y 都是整数)$ ，规定： $k = \frac{F (s)}{F (t)}$ ，当 $3 (F (s) + F (t))$ 是完全平方数时（如果一个数a是另一个整数b的平方，则称数a是完全平方数），求k的最小值.

查看试题解析