湖南省郴州市永兴县五校联考2022-2023学年七年级上学期期末考试数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 在下列单项式 , , , 中,次数是的是( )A、 B、 C、 D、3. 月日,国家统计局公布的全国粮食生产数据显示,年全国粮食总产量达亿斤,比上年增加亿斤,增长 , 全年粮食产量再创新高,连续年保持在万亿斤以上.将亿斤换成以斤为单位后,再用科学记数法表示为( )A、 B、 C、 D、4. 下列运用等式的性质进行的变形,错误的是( )A、如果 , 则 B、如果 , 则 C、如果 , 则 D、如果 , 则5. 下列关于角的说法,正确的是( )A、一个平角等于 B、的补角是 C、一个角的补角一定大于这个角 D、两个锐角的和一定为钝角6. 把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、三角形两边之和大于第三边7. 若是一元一次方程,则m等于( )A、1 B、2 C、1或2 D、任何数8. 有理数 , , 在数轴上的位置如图所示,式子化简为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 比较大小:.10. 列代数式:一个两位数,它的十位数字是 , 个位数字是则这个两位数是.11. 一个多项式加上得到 , 则这个多项式是.12. 如图:一个正方体的侧面展开图,相对的面是一对相反数,则.
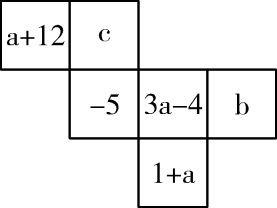 13. 如图:和均为直角,已知 , 则.
13. 如图:和均为直角,已知 , 则. 14. 若|x|=9,则x= .15. 已知 , 则的值为.16. , , , 为有理数,先规定一种新的运算: , 那么 , .
14. 若|x|=9,则x= .15. 已知 , 则的值为.16. , , , 为有理数,先规定一种新的运算: , 那么 , .三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 先化简再求值 , 其中 , .20. 如图,直线AB和直线CD相交于点O,OB平分∠EOD.
 (1)、若∠EOC=110°,求∠BOD的度数;(2)、若∠DOE∶∠EOC=2∶3,求∠AOC的度数.21. 一批水果的标准质量是30千克,超出标准质量记为正,低于标准质量记为负,现记录如下: , , , , , , , .(1)、这批水果总共有多少千克?(2)、第一天按每千克价格10元卖出了这批水果的一半,第二天为了吸引顾客把第一天卖水果的价格打九折后作为新的价格,卖完了剩下的水果,请计算一下这批水果一共卖了多少钱?22. 某超市为了解顾客对白面馒头、大肉包、水饺、米粉、葱油饼(以下分别用A,B.C,D,E表示)这五种早点的喜爱情况,对顾客进行了调查,并将调查结果绘制成如下两幅不完整统计图.
(1)、若∠EOC=110°,求∠BOD的度数;(2)、若∠DOE∶∠EOC=2∶3,求∠AOC的度数.21. 一批水果的标准质量是30千克,超出标准质量记为正,低于标准质量记为负,现记录如下: , , , , , , , .(1)、这批水果总共有多少千克?(2)、第一天按每千克价格10元卖出了这批水果的一半,第二天为了吸引顾客把第一天卖水果的价格打九折后作为新的价格,卖完了剩下的水果,请计算一下这批水果一共卖了多少钱?22. 某超市为了解顾客对白面馒头、大肉包、水饺、米粉、葱油饼(以下分别用A,B.C,D,E表示)这五种早点的喜爱情况,对顾客进行了调查,并将调查结果绘制成如下两幅不完整统计图.
根据以上统计图解答问题:
(1)、本次被调查的顾客共有 ▲ 人次;补全条形统计图;(2)、扇形统计图中白面馒头对应的圆心角是度;(3)、若某天有1200人次购买了这五种早点,估计其中喜爱大肉包的有多少人次?23. 列方程解应用题.冬季取暖要确保防火安全.为了满足顾客的需要,某购物广场用25000元购进A,B两种新型防火取暖器共50个,这两种取暖器的进价、标价如下表所示:
价格
类型
A型
B型
进价(元/个)
400
650
标价(元/个)
600
m
(1)、A,B两种新型取暖器分别购进多少个?(2)、若A型取暖器按标价的七五折出售,B型取暖器每台在标价的基础上降价75元出售,这批取暖器全部售完后商场共获利4000元,请求出表格中m的值.24. 一串图形按如图所示的规律排列.
(说明:下列所指的小正方形都是与第1个图形一样大小的正方形)
(1)、第5个图形中有几个小正方形?第6个图形呢?(2)、求出第 个图形中小正方形的个数.(3)、求出第20个图形中小正方形的个数.(4)、是否存在某个图形,其小正方形的个数恰好是下列各数:① 5050;②1000.给出你的判断,并说明理由.25. 对于有理数 , , , , 若 , 则称和关于的“美好关联数”为 , 例如,则 , 则2和3关于1的“美好关联数”为3.(1)、和5关于2的“美好关联数”为;(2)、若和2关于3的“美好关联数”为4,求的值;(3)、若和关于1的“美好关联数”为1,和关于2的“美好关联数”为1,和关于3的“美好关联数”为1,…,和的“美好关联数”为1,….①的最小值为 ▲ ;
②的值为 ▲ .
26.(1)、特例感知:如图①,已知线段MN=30cm,AB=2cm,线段AB在线段MN上运动(点A不超过点M,点B不超过点N),点C和点D分别是AM,BN的中点.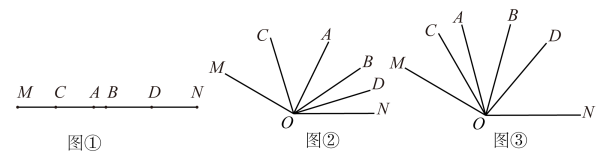
①若AM=16cm,则CD= ▲ cm;
②线段AB运动时,试判断线段CD的长度是否发生变化?如果不变,请求出CD的长度,如果变化,请说明理由.
(2)、知识迁移:我们发现角的很多规律和线段一样,如图②,已知∠AOB在∠MON内部转动,射线OC和射线OD分别平分∠AOM和∠BON.①若∠MON=150°,∠AOB=30°,求∠COD= ▲ S度.
②请你猜想∠AOB,∠COD和∠MON三个角有怎样的数量关系.请说明理由.
(3)、类比探究:如图③,∠AOB在∠MON内部转动,若∠MON=150°,∠AOB=30°, , 用含有k的式子表示的度数.(直接写出计算结果)