河南省南阳市宛城区2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-02-01 类型:期末考试
一、单选题
-
1. 如果零上2℃记作+2℃,那么零下3℃记作()A、-3℃ B、-2℃ C、+3℃ D、+2℃2. 下列说法正确的是( )A、 一定是负数 B、 是二次三项式 C、-5不是单项式 D、 的系数是3. 树叶上有许多气孔,在阳光下,这些气孔一面排出氧气和蒸腾水分,一面吸入二氧化碳,一个气孔在一秒钟内能吸进亿个二氧化碳分子,用科学记数法表示亿为( )A、 B、 C、 D、4. 如图所示,下列结论中正确的是 ( )
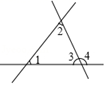 A、 和 是同位角 B、 和 是同旁内角 C、 和 是内错角 D、 和 是对顶角5. 在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )A、用两颗钉子就可以把木条固定在墙上; B、当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下; C、把弯曲的公路改直,就能缩短路程; D、在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标.6. 下面去括号正确的是( )A、 B、 C、 D、7. 若整式经过化简后结果等于4,则的值为( )A、 B、8 C、 D、98. 如图是由五个完全相同的小正方体组成的几何体,若将最左边的小正方体拿掉,则下列结论正确的是( )
A、 和 是同位角 B、 和 是同旁内角 C、 和 是内错角 D、 和 是对顶角5. 在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )A、用两颗钉子就可以把木条固定在墙上; B、当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下; C、把弯曲的公路改直,就能缩短路程; D、在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标.6. 下面去括号正确的是( )A、 B、 C、 D、7. 若整式经过化简后结果等于4,则的值为( )A、 B、8 C、 D、98. 如图是由五个完全相同的小正方体组成的几何体,若将最左边的小正方体拿掉,则下列结论正确的是( ) A、主视图不变 B、左视图不变 C、俯视图不变 D、三视图不变9. 如图,下列能判定∥的条件有几个( )(1)、 (2)(3) (4).
A、主视图不变 B、左视图不变 C、俯视图不变 D、三视图不变9. 如图,下列能判定∥的条件有几个( )(1)、 (2)(3) (4).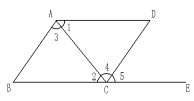 A、4 B、3 C、2 D、110. 若 、 互为相反数, 、 互为倒数, 的绝对值为 ,则 的值为( )A、 B、 C、 D、 或
A、4 B、3 C、2 D、110. 若 、 互为相反数, 、 互为倒数, 的绝对值为 ,则 的值为( )A、 B、 C、 D、 或二、填空题
-
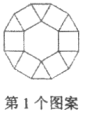
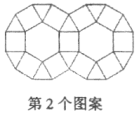
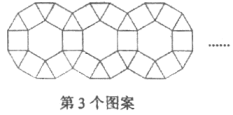
11. 把多项式 按x的升幂排列为 .12. 已知 和 的两边分别平行,若 ,则 .13. 用一生活情景描述2a+3b的实际意义:14. 如图是用正三角形、正方形、正六边形设计的一组图案,按照规律,第个图案中正三角形的个数是.
 15. 如图, 为一长条形纸带, ,将 沿 折叠, 、 两点分别与 、 对应.若 ,则 .
15. 如图, 为一长条形纸带, ,将 沿 折叠, 、 两点分别与 、 对应.若 ,则 .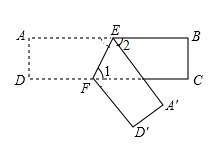
三、解答题
-
16. 计算:(1)、 ;(2)、 ;17. 计算:一个整式A与多项式x2-x-1的和是多项式-2x2-3x+4.(1)、请你求出整式A;(2)、当x=2时求整式A的值18. 先阅读下列材料,然后解答问题.
探究:用的幂的形式表示am•an的结果(m、为正整数).
分析:根据乘方的意义,am•an==am+n.
(1)、请根据以上结论填空:36×38= ,52×53×57= , (a+b)3•(a+b)5= ;(2)、仿照以上的分析过程,用的幂的形式表示(am)n的结果(提示:将am看成一个整体).19. 如图,已知 , 垂足分别为D、F,=180°,试说明:.请补充说明过程,并在括号内填上相应的理由.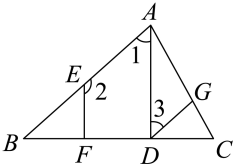
解:∵(已知)
∴( ),
∴( ),
∴ ▲ +∠2 =180°( ).
又∵( ),
∴∠1=∠3( ),
∴ ▲ ( ),
∴( ).
20. 如图是一些棱长为1cm 的小立方块组成的几何体.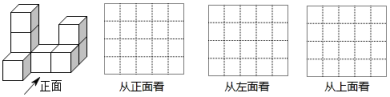 (1)、请画出从正面看,从左面看,从上面看到的这个几何体的形状图.(2)、该几何体的表面积是cm2 .(3)、如果把它拼成一个无空隙的正方体,则至少还需要同样的小立方块块.(4)、如果保持从正面和上面看到的形状不变,最多可以再添加个小立方块.21. 如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)、请画出从正面看,从左面看,从上面看到的这个几何体的形状图.(2)、该几何体的表面积是cm2 .(3)、如果把它拼成一个无空隙的正方体,则至少还需要同样的小立方块块.(4)、如果保持从正面和上面看到的形状不变,最多可以再添加个小立方块.21. 如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.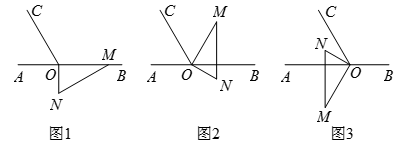 (1)、如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC,此时∠AOM=度;∠BON=度.(2)、如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由.(3)、将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是秒.22. 某商店将进货价为每件元的商品以每件元的销售价售出,平均每月能售出件.市场调查发现,当每件商品售价每上涨元时,其销售量将减少件.若设每件商品的销售价元.(1)、试用含的代数式填空:
(1)、如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC,此时∠AOM=度;∠BON=度.(2)、如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由.(3)、将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是秒.22. 某商店将进货价为每件元的商品以每件元的销售价售出,平均每月能售出件.市场调查发现,当每件商品售价每上涨元时,其销售量将减少件.若设每件商品的销售价元.(1)、试用含的代数式填空:①涨价后,每件商品的利润为元;
②涨价后,商店该商品平均每月的销售量为件;(填化简后的结果)
③涨价后,商店平均每月销售利润为元;
(2)、如果这家商店要想平均每月销售利润达到元,甲同学说:在原售价每件元的基础上再上涨元,可以完成任务.乙同学说:不用涨那么多,在原售价每件元的基础上再上涨元就可以了.请你根据计算说明甲同学与乙同学的说法是否正确.23. 【新知理解】如图①,点在线段上,图中的三条线段 , 和.若其中一条线段的长度是另外一条线段长度的2倍,则称点是线段的“巧点”.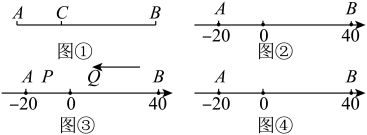 (1)、填空:线段的中点这条线段的巧点;(填“是”或“不是”或“不确定是”)(2)、【问题解决】如图②,点和在数轴上表示的数分别是和 , 点是线段的巧点,求点在数轴上表示的数.(3)、【应用拓展】在(2)的条件下,动点从点发,以每秒2个单位长度的速度沿向点匀速运动;动点从点出发,以每秒4个单位长度的速度沿向点匀速运动.点同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为秒,当t为何值时,、三点中,其中一点恰好是另外两点为端点的线段的巧点?并求出此时巧点在数轴上表示的数.
(1)、填空:线段的中点这条线段的巧点;(填“是”或“不是”或“不确定是”)(2)、【问题解决】如图②,点和在数轴上表示的数分别是和 , 点是线段的巧点,求点在数轴上表示的数.(3)、【应用拓展】在(2)的条件下,动点从点发,以每秒2个单位长度的速度沿向点匀速运动;动点从点出发,以每秒4个单位长度的速度沿向点匀速运动.点同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为秒,当t为何值时,、三点中,其中一点恰好是另外两点为端点的线段的巧点?并求出此时巧点在数轴上表示的数.