2023年中考数学复习考点一遍过——图形认识初步
试卷更新日期:2023-01-30 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
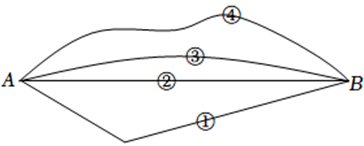 A、① B、② C、③ D、④2. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( )
A、① B、② C、③ D、④2. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( ) A、 B、 C、 D、3. 如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
A、 B、 C、 D、3. 如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )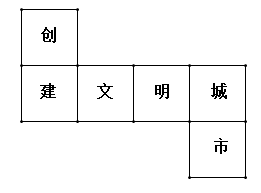 A、文 B、明 C、城 D、市4. 如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
A、文 B、明 C、城 D、市4. 如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )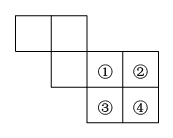 A、① B、② C、③ D、④5. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A、① B、② C、③ D、④5. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )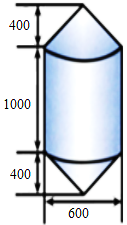 A、282.6 B、282600000 C、357.96 D、3579600006. 如图,将矩形绕着它的一边所在的直线1旋转一周,可以得到的立体图形是( )
A、282.6 B、282600000 C、357.96 D、3579600006. 如图,将矩形绕着它的一边所在的直线1旋转一周,可以得到的立体图形是( ) A、
A、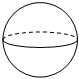 B、
B、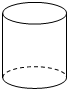 C、
C、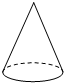 D、
D、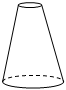 7. 如图, , 点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( )
7. 如图, , 点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( ) A、45° B、50° C、57.5° D、65°8. 如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A、45° B、50° C、57.5° D、65°8. 如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )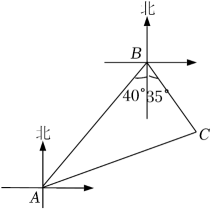 A、北偏东70° B、北偏东75° C、南偏西70° D、南偏西20°9. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )
A、北偏东70° B、北偏东75° C、南偏西70° D、南偏西20°9. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )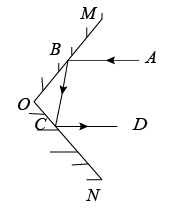 A、 B、 C、 D、10. 如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A、 B、 C、 D、10. 如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )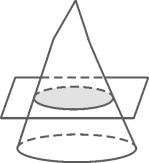 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每题3分,共24分)
-
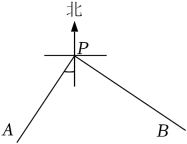
11. 如图,PA,PB表示以P为起点的两条公路,其中公路PA的走向是南偏西34 , 公路PB的走向是南偏东56 , 则这两条公路的夹角∠APB=°.
 12. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).13. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
12. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).13. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .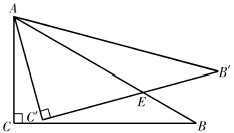 14. 如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为
14. 如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为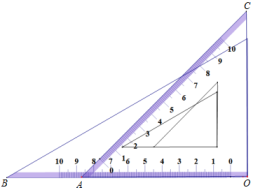 15. 如图,点C是线段AB的中点,若AC=2cm,则AB=cm.
15. 如图,点C是线段AB的中点,若AC=2cm,则AB=cm.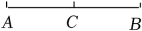 16. 已知∠α=60°,则∠α的余角等于度.17. 如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是.
16. 已知∠α=60°,则∠α的余角等于度.17. 如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是.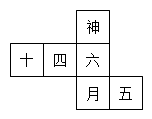 18. 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)”,如图所示.问题:此图中,正方形一条对角线与⊙相交于点、(点在点的右上方),若的长度为10丈,⊙的半径为2丈,则的长度为丈.
18. 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)”,如图所示.问题:此图中,正方形一条对角线与⊙相交于点、(点在点的右上方),若的长度为10丈,⊙的半径为2丈,则的长度为丈.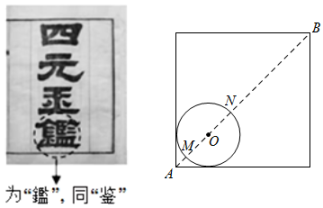
三、解答题(共8题,共66分)
-
19. 已知,如图, , 两点把线段分成三部分,为的中点, , 求的长.
 20. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
20. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数. 21. 如图所示,已知 , 从点出发的一条射线满足 , 是的平分线,是的平分线,请补全图形(画出正确的草图即可),并求出的大小.
21. 如图所示,已知 , 从点出发的一条射线满足 , 是的平分线,是的平分线,请补全图形(画出正确的草图即可),并求出的大小.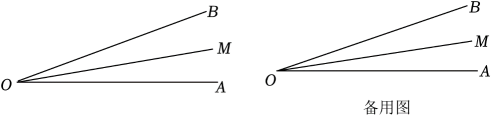 22. 如图
22. 如图
 (1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).23. 如图
(1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).23. 如图 (1)、如图,平面上有四个点A,B,C,D,按照以下要求作图:
(1)、如图,平面上有四个点A,B,C,D,按照以下要求作图:①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)、图中共有条线段.24. 如图,一个边长为10cm的无盖正方体可以展开成下面的平面图形.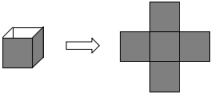
 (1)、这个表面展开图的面积是cm2;(2)、将一个无盖正方体展开成平面图形的过程中,需要剪开条棱;(3)、你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出所有可能的图形(把需要的小正方形涂上阴影).25. 如图所示,是由10个完全相同的棱长为1cm的小正方体组成的几何体.
(1)、这个表面展开图的面积是cm2;(2)、将一个无盖正方体展开成平面图形的过程中,需要剪开条棱;(3)、你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出所有可能的图形(把需要的小正方形涂上阴影).25. 如图所示,是由10个完全相同的棱长为1cm的小正方体组成的几何体. (1)、请分别画出从正面、上面、左面三个方向看到的图形;(2)、这个几何体的表面积是(包括底部).26. 如图所示,以直线上的一点为端点,在直线的上方作射线 , 使 , 将一块直角三角尺的直角顶点放在点处,且直角三角尺在直线的上方.设 .
(1)、请分别画出从正面、上面、左面三个方向看到的图形;(2)、这个几何体的表面积是(包括底部).26. 如图所示,以直线上的一点为端点,在直线的上方作射线 , 使 , 将一块直角三角尺的直角顶点放在点处,且直角三角尺在直线的上方.设 . (1)、当n=30时,求的大小;(2)、当恰好平分时,求n的值;(3)、当时,嘉嘉认为与的差为定值,淇淇认为与的和为定值,且二人求得的定值相同,均为 , 老师说,要使两人的说法都正确,需要对n分别附加条件.请你补充这个条件:
(1)、当n=30时,求的大小;(2)、当恰好平分时,求n的值;(3)、当时,嘉嘉认为与的差为定值,淇淇认为与的和为定值,且二人求得的定值相同,均为 , 老师说,要使两人的说法都正确,需要对n分别附加条件.请你补充这个条件:当满足时,;
当满足时, .