2022-2023学年上海市九年级上学期数学期末模拟卷

试卷更新日期：2023-01-29 类型：期末考试

进入出卷网下载

一、单选题（每题4分，共24分）

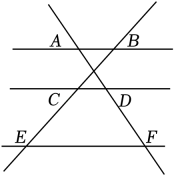
1. 如图，已知AB∥CD∥EF，AD：DF＝2：3，BE＝15，那么BC的长为（）

A、5 B、6 C、7 D、8

查看试题解析
2. 已知：点C在线段AB上，且AC = 2BC，那么下列等式一定正确的是（）

A、 $\overset{⇀}{A C} + 2 \overset{⇀}{B C} = \frac{4}{3} \overset{⇀}{A B}$ B、 $\overset{⇀}{A C} - 2 \overset{⇀}{B C} = \overset{⇀}{0}$ C、 $| \overset{⇀}{A C} + \overset{⇀}{B C} | = | \overset{⇀}{B C} |$ D、 $| \overset{⇀}{A C} - \overset{⇀}{B C} | = | \overset{⇀}{B C} |$

查看试题解析
3. 在Rt△ABC中，∠C=90°，AB=5，AC=4．下列四个选项，正确的是（）

A、tanB= $\frac{3}{4}$ B、sinB= $\frac{4}{3}$ C、sinB= $\frac{4}{5}$ D、cosB= $\frac{4}{5}$

查看试题解析
4. 下列函数中，是二次函数的是（）

A、y＝- $\frac{11}{x^{2}}$ B、y＝2x²-x+2 C、y＝ $\frac{1}{x}$ D、y＝2x+2

查看试题解析
5. 已知点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 均在抛物线 $y = x^{2} - 1$ 上，下列说法正确的是（）

A、若 $x_{1} = - x_{2}$ ，则 $y_{1} = - y_{2}$ B、若 $y_{1} = y_{2}$ ，则 $x_{1} = x_{2}$ C、若 $x_{1} < x_{2} < 0$ ，则 $y_{1} < y_{2}$ D、若 $0 < x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$

查看试题解析
6. 如图，如果 $∠ B = ∠ D$ ，那么添加下列一个条件后，仍不能确定 $△ A B C ∽ △ A D E$ 的是（）

A、 $∠ C = ∠ A E D$ B、 $∠ B A C = ∠ D A E$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $∠ B A D = ∠ C A E$

查看试题解析

二、填空题（每题4分，共48分）

7. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{e}{5} = \frac{1}{2} (b + d + 5 \neq 0)$ ，则 $\frac{a + c + e}{b + d + 5} =$ .

查看试题解析
8. 在比例尺为1：38000的扬州旅游地图上，某条道路的长为6cm，则这条道路的实际长度为km．

查看试题解析
9. 如图，若AC是BC与AB的比例中项，AB=4，求AC=.

查看试题解析
10. 已知 $\vec{a}$ 与单位向量 $\vec{e}$ 的方向相同，且长度为 $5$ ，那么用 $\vec{e}$ 表示 $\vec{a}$ $=$ ．

查看试题解析
11. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，若 $\frac{A C}{A B} = \frac{4}{5}$ ，则 $s i n A =$ ．

查看试题解析
12. 如图，大坝横截面的迎水坡AB的坡比为1：2（即BC：AC＝1：2），若坡面AB的水平宽度AC为12米，则斜坡AB的长为米.

查看试题解析
13. 已知二次函数 $y = 3 (x - 3) (x + 2)$ ，则该函数对称轴为直线.

查看试题解析
14. 已知二次函数 $y = - 3 x^{2} + (2 m - 1) x + 1$ ，当 $x > - 2$ 时，y随x的增大而减小，则m的取值范围是 .

查看试题解析
15. 如图，在△ABC中，AB：AC=7：3，∠BAC的平分线交BC于点E，过点B作AE的垂线段，垂足为D，则AE：ED= ．

查看试题解析
16. 如图所示，某校数学兴趣小组利用自制的直角三角形硬纸板 $D E F$ 来测量操场旗杆 $A B$ 的高度，他们通过调整测量位置，使斜边 $D F$ 与地面保持平行，并使边 $D E$ 与旗杆顶点 $A$ 在同一直线上，已知 $D E = 0.5$ 米， $E F = 0.25$ 米，目测点 $D$ 到地面的距离 $D G = 1.5$ 米，到旗杆水平的距离 $D C = 20$ 米，则旗杆的高度为米．

查看试题解析
17. 工人师傅在修茸一人字架屋顶BAC时需要加固，计划焊接三根钢条AD，DE，FG．在如图所示的△ABC中，AB=AC=10，BC=12，AD⊥BC于点D，点E，F，G分别是AB，BD，AC上的点，连接DE，GF，交于点H，GF与AD交于点M，当H为FM的中点，BF∶CF=1∶5，AG：AE=5：7时，△AGM的面积为．

查看试题解析
18. 如图，将一个Rt△ABC形状的楔子从木桩的底点P沿水平方向打入木桩底下，使木桩向上移动．已知楔子斜面的倾斜角为15°，若楔子沿水平方向前进6cm（如箭头所示），则木桩上升了 .（结果可含有三角函数）

查看试题解析

三、计算题（共10分）

19. 计算：2|1﹣sin60°|+ $\frac{\tan 45 °}{\cot 30 ° - 2 \cos 45 °}$ ．

查看试题解析

四、综合题（共2题，共20分）

20. 如图是二次函数y＝a(x＋1)²＋2的图象的一部分，根据图象回答下列问题：

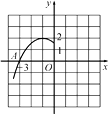(1)、抛物线与x轴的一个交点A的坐标是，则抛物线与x轴的另一个交点B的坐标是；

(2)、确定a的值；

(3)、设抛物线的顶点是P，试求△PAB的面积．

查看试题解析
21. 在平面直角坐标系xOy中，过点（0，2）且平行于x轴的直线，与直线y=x﹣1交于点A，点A关于直线x=1的对称点为B，抛物线C₁：y=x²+bx+c经过点A，B．

(1)、求点A，B的坐标；

(2)、求抛物线C₁的表达式及顶点坐标；

(3)、若抛物线C₂：y=ax²（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围．

查看试题解析

五、解答题（共4题，共48分）

22. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， D是 $A B$ 的中点， $E D ⊥ A B$ 交AC于点E， $t a n ∠ E B C = \frac{3}{4}$ ．求 $∠ A B E$ 的正切值．

查看试题解析
23. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度，在河的北岸边点A处，测得河的南岸边点B处在其南偏东 $45 °$ 方向，然后向北走20米到达点C处，测得点B在点C的南偏东 $33 °$ 方向，求出这段河的宽度(结果精确到1米，参考数据： $\sin 33 ° = 0.54$ ， $\cos 33 ° \approx 0.84$ ， $\tan 33 ° = 0.65$ ， $\sqrt{2} \approx 1.41$ )

查看试题解析
24. 如图，△ABC中，∠BAC=90°，AB=AC，D在BC上，E在AC上，且∠ADE=45度．

(1)、求证：△ABD∽△DCE．

(2)、当D在什么位置时，△ABD≌△DCE．

查看试题解析
25. 如图，△ABC是一锐角三角形余料，边BC=16cm，高AD=24cm，要加工成矩形零件，使矩形的一边在BC上，其余两个顶点E、F分别在AB、AC上．

求：

(1)、AK为何值时，矩形EFGH是正方形？

(2)、若设AK=x，S_EFGH=y，试写出y与x的函数解析式．

(3)、x为何值时，S_EFGH达到最大值．

查看试题解析