2023年中考数学精选真题实战测试37 平行四边形 A
试卷更新日期:2023-01-29 类型:二轮复习
一、单选题(每题3分,共30分)
-
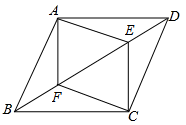
1. 如图,四边形 的内角和等于( )
 A、 B、 C、 D、2. 依据所标数据,下列一定为平行四边形的是()A、
A、 B、 C、 D、2. 依据所标数据,下列一定为平行四边形的是()A、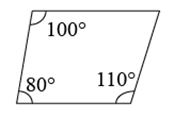 B、
B、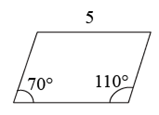 C、
C、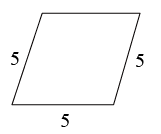 D、
D、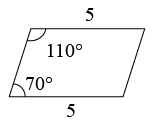 3. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )
3. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )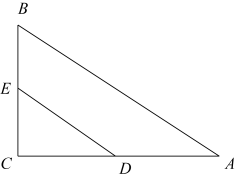 A、70° B、60° C、30° D、20°4. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )
A、70° B、60° C、30° D、20°4. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )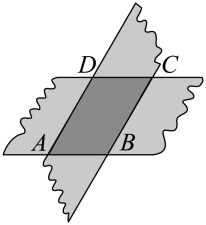 A、四边形周长不变 B、 C、四边形面积不变 D、5. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )
A、四边形周长不变 B、 C、四边形面积不变 D、5. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )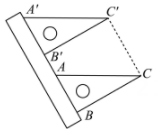 A、96 B、 C、192 D、6. 如图,在中, , 是上的点,交于点 , 交于点 , 那么四边形的周长是( )
A、96 B、 C、192 D、6. 如图,在中, , 是上的点,交于点 , 交于点 , 那么四边形的周长是( )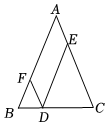 A、5 B、10 C、15 D、207. 如图,在四边形 中,点 , , , 分别是 , , , 边上的中点,则下列结论一定正确的是( )
A、5 B、10 C、15 D、207. 如图,在四边形 中,点 , , , 分别是 , , , 边上的中点,则下列结论一定正确的是( )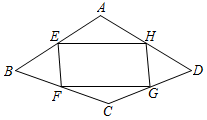 A、四边形 是矩形 B、四边形 的内角和小于四边形 的内角和 C、四边形 的周长等于四边形 的对角线长度之和 D、四边形 的面积等于四边形 面积的8. 如图,▱ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
A、四边形 是矩形 B、四边形 的内角和小于四边形 的内角和 C、四边形 的周长等于四边形 的对角线长度之和 D、四边形 的面积等于四边形 面积的8. 如图,▱ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )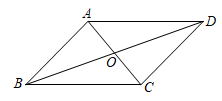 A、OB=OD B、AB=BC C、AC⊥BD D、∠ABD=∠CBD9. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
A、OB=OD B、AB=BC C、AC⊥BD D、∠ABD=∠CBD9. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )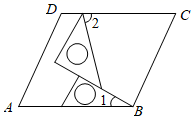 A、 B、 C、 D、10. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )
A、 B、 C、 D、10. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )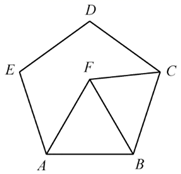 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
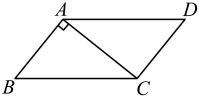
11. 如图,在中, , 若 , 则的度数是.
 12. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.
12. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.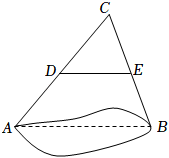 13. 一个正n边形的一个外角等于36°,则n= .14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
13. 一个正n边形的一个外角等于36°,则n= .14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .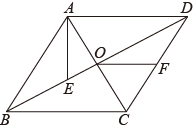 15. 如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是.(只需写一种情况)
15. 如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是.(只需写一种情况)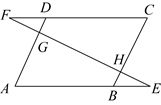 16. 一个多边形的每一个外角都等于60°,则这个多边形的内角和为 度.
16. 一个多边形的每一个外角都等于60°,则这个多边形的内角和为 度.三、解答题(共8题,共72分)
-
17. 如图,在▱ABCD中,DF平分∠ADC,交AB于点F,BEDF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.
 18. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.
18. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.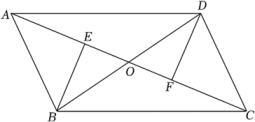 19. 如图,四边形ABCD中,AB=DC,将对角线AC向两端分别延长至点E,F,使AE=CF.连接BE,DF,若BE=DF.证明:四边形ABCD是平行四边形.
19. 如图,四边形ABCD中,AB=DC,将对角线AC向两端分别延长至点E,F,使AE=CF.连接BE,DF,若BE=DF.证明:四边形ABCD是平行四边形. 20. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
20. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.(注:如果选择多个条件分别解答,按第一个解答计分.)
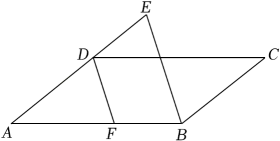
21. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证: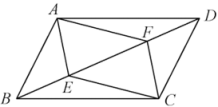 (1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.22. 如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且 ,连接AF,CE,AC,EF,且AC与EF相交于点O.
(1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.22. 如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且 ,连接AF,CE,AC,EF,且AC与EF相交于点O.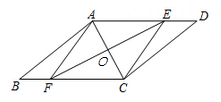 (1)、求证:四边形AFCE是平行四边形;(2)、若AC平分 , ,求四边形AFCE的面积.
(1)、求证:四边形AFCE是平行四边形;(2)、若AC平分 , ,求四边形AFCE的面积.