2023年中考数学一轮复习-全等三角形八大模型汇总(通用)
试卷更新日期:2023-01-28 类型:一轮复习
一、对称模型
-
1. 如图,点B、F、C、E在同一条直线上,AB⊥BE,DE⊥BE,AB=DE,BF=EC,求证:∠A=∠D.
 2. 已知:如图,点D在线段AC上,点B在线段AE上,AE=AC,BE=DC,求证:∠E=∠C.
2. 已知:如图,点D在线段AC上,点B在线段AE上,AE=AC,BE=DC,求证:∠E=∠C. 3. 如图,在中,与的平分线相交于点O,AO的延长线交于点D,.求证:.
3. 如图,在中,与的平分线相交于点O,AO的延长线交于点D,.求证:. 4. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:.
4. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:. 5. 如图,已知 , 相交于点 , 且 , .
5. 如图,已知 , 相交于点 , 且 , . (1)、求证:≌.(2)、若 , 求的度数.
(1)、求证:≌.(2)、若 , 求的度数.二、平移模型
-
6. 如图,点B,E,C,F在同一直线上, , , . 线段与有什么数量关系?请说明理由.
 7. 如图,点A,F,C,D在同一直线上, , 请你再添加一个条件,使得 , 并证明.
7. 如图,点A,F,C,D在同一直线上, , 请你再添加一个条件,使得 , 并证明. 8. 已知:如图,在△ADF和△BCE中,点B,F,E,D依次在一条直线上,若AF∥CE,∠B=4D,BF=DE,求证:AF=CE.
8. 已知:如图,在△ADF和△BCE中,点B,F,E,D依次在一条直线上,若AF∥CE,∠B=4D,BF=DE,求证:AF=CE.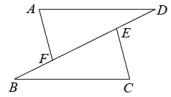 9. 如图,点 , 在上,且 , , .
9. 如图,点 , 在上,且 , , . (1)、求证: .(2)、连结 , 若 , , , 求的长度.
(1)、求证: .(2)、连结 , 若 , , , 求的长度.三、角平分线模型
-
10. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.
 11. 如图, , M是的中点,平分 , 且 , 求的度数
11. 如图, , M是的中点,平分 , 且 , 求的度数 12. 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
12. 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF. 13. 如图,在中, , , , , , 动点E以的速度从A点向F点运动,动点G以的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
13. 如图,在中, , , , , , 动点E以的速度从A点向F点运动,动点G以的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t. (1)、求证:;(2)、当t取何值时,与全等.14. 综合与实践:
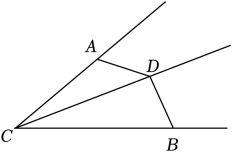
(1)、求证:;(2)、当t取何值时,与全等.14. 综合与实践:问题情境:已知是的平分线,P是射线上的一点,点C,D分别在射线 , 上,连接 .
 (1)、初步探究:如图1,当 , 时,与的数量关系是;(2)、深入探究:如图2,点C,D分别在射线 , 上运动,且 , 当时,与在(1)中的数量关系还成立吗?请说明理由;(3)、拓展应用:如图3,如果点C在射线上运动,且 , 当时,点D落在了射线的反向延长线上,若点P到的距离为3, , 求的长(直接写出答案).
(1)、初步探究:如图1,当 , 时,与的数量关系是;(2)、深入探究:如图2,点C,D分别在射线 , 上运动,且 , 当时,与在(1)中的数量关系还成立吗?请说明理由;(3)、拓展应用:如图3,如果点C在射线上运动,且 , 当时,点D落在了射线的反向延长线上,若点P到的距离为3, , 求的长(直接写出答案).四、手拉手模型
-
15. 如图,在中以为边分别作正方形、 , 连接 . 证明: .
 16. 在中,以AB为边作等边 , 以AC为边作等边 , 连接 , 求证: .
16. 在中,以AB为边作等边 , 以AC为边作等边 , 连接 , 求证: .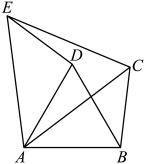 17. 如图,中, , , D为外一点, , 交于点E,F为上一点, , 过点F作交于点G.
17. 如图,中, , , D为外一点, , 交于点E,F为上一点, , 过点F作交于点G. (1)、求证:;(2)、求证:是等腰直角三角形;(3)、若 , 求的度数.18. 已知和中, , , , 与交于点 .
(1)、求证:;(2)、求证:是等腰直角三角形;(3)、若 , 求的度数.18. 已知和中, , , , 与交于点 . (1)、如图1当时.求证:
(1)、如图1当时.求证:≌;
;
(2)、如图2当时,直接写出的度数为;(3)、如图3,直接写出的度数为 用含的式子表示 .19. 如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α.以OC为边作等边△OCD,连接AD.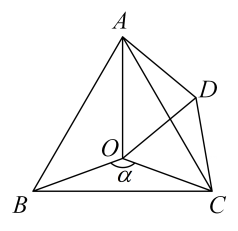 (1)、求证:△BOC≌△ADC;(2)、当a=150°时,试判断△AOD的形状,并说明理由;(3)、探究:当α为多少度时,△AOD是等腰三角形?
(1)、求证:△BOC≌△ADC;(2)、当a=150°时,试判断△AOD的形状,并说明理由;(3)、探究:当α为多少度时,△AOD是等腰三角形?五、倍长中线模型
-
20. 如图,在中,是中线,于点E,于点E,于点F,交AD的延长线于点F,求证: .
 21. 如图 , 是的中线.
21. 如图 , 是的中线.求证: .
请将下面的推理过程补充完整:
证明:如图 , 延长到点 , 使 , 连接 .
∵是的中线,
∴ .
在和中,
,
∴( ).
∴ ▲ (全等三角形的对应边相等).
∴在中,( ),
∴ .
即 .
 22. 如图,在中,是边上的高线,是边上的中线,于 G, .
22. 如图,在中,是边上的高线,是边上的中线,于 G, . (1)、求证:;(2)、已知 , 求面积.23.(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
(1)、求证:;(2)、已知 , 求面积.23.(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
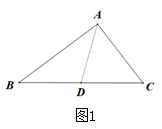 (2)、【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.
(2)、【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长. (3)、【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
(3)、【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
六、一线三等角模型
-
24. 如图,点E在上,于点A,于点B, , .
 (1)、说明的理由;(2)、求的度数.25. 如图, , 射线 , 且 , 点是线段不与点、重合上的动点,过点作交射线于点 , 连接.
(1)、说明的理由;(2)、求的度数.25. 如图, , 射线 , 且 , 点是线段不与点、重合上的动点,过点作交射线于点 , 连接. (1)、如图1,若 , , 求的长.(2)、如图2,若平分 ,
(1)、如图1,若 , , 求的长.(2)、如图2,若平分 ,试猜测和的数量关系,并说明理由;
若的面积为5,求四边形的面积.
(3)、如图3,①已知点是网格中的格点,若三角形是以为底边的等腰三角形,那么这样的点共有 ▲ 个;
②在网格中找出一个点 , 使得点到点 , 和点 , 的距离分别相等,请在网格中标注点保留作图痕迹
26. 如图,在中, , , 点D是线段上任意一点,连接 , 作 , 交线段于点E. (1)、若 , 求和的度数;(2)、若 , 求证: .27. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)、若 , 求和的度数;(2)、若 , 求证: .27. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.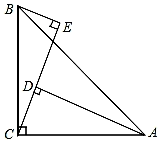 (1)、求证:△ADC≌△CEB.(2)、AD=5cm,DE=3cm,求BE的长度.28. 如图:
(1)、求证:△ADC≌△CEB.(2)、AD=5cm,DE=3cm,求BE的长度.28. 如图: (1)、模型的发现:
(1)、模型的发现:如图1,在中, , , 直线经过点 , 且、两点在直线的同侧,直线 , 直线 , 垂足分别为点 , . 请直接写出、和的数量关系.
(2)、模型的迁移1:位置的改变如图2,在(1)的条件下,若 , 两点在直线的异侧,请说明、和的关系,并证明.
(3)、模型的迁移2:角度的改变如图3,在(1)的条件下,若三个直角都变为了相等的钝角,即 , 其中 , (1)的结论还成立吗?若成立,请你给出证明;若不成立,请说明、和的关系,并证明.
七、截长补短模型
-
29.(1)、如图1,在四边形中, , , E、F分别是、上的点,且 , 探究图中、、之间的数量关系.
小芮同学探究此问题的方法是:延长到点G,使 . 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是;
 (2)、如图2,若在四边形中, , , E、F分别是、上的点,且 , 上述结论是否仍然成立,并说明理由.
(2)、如图2,若在四边形中, , , E、F分别是、上的点,且 , 上述结论是否仍然成立,并说明理由. (3)、已知在四边形中, , , 若点E在的延长线上,点F在的延长线上,如图3所示,仍然满足 , 请直接写出与的数量关系.
(3)、已知在四边形中, , , 若点E在的延长线上,点F在的延长线上,如图3所示,仍然满足 , 请直接写出与的数量关系. 30. 问题背景:
30. 问题背景: (1)、如图1,在四边形中, , , , , 分别是 , 上的点,且 , 探究图中线段、、之间的数量关系,嘉琪同学探究此问题的方法是:延长到点 , 使 , 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是 .(2)、探索延伸:①如图2,若在四边形中, , , 、分别是 , 上的点,且 , 上述结论是否仍然成立,并说明理由.
(1)、如图1,在四边形中, , , , , 分别是 , 上的点,且 , 探究图中线段、、之间的数量关系,嘉琪同学探究此问题的方法是:延长到点 , 使 , 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是 .(2)、探索延伸:①如图2,若在四边形中, , , 、分别是 , 上的点,且 , 上述结论是否仍然成立,并说明理由.②如图2,若五边形的面积为30, , , 直接写出点到的距离.
31.(1)、【问题引领】
问题1:如图1,在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接CG,先证明CBE≌CDG,再证明CEF≌CGF.他得出的正确结论是 .
 (2)、
(2)、
【探究思考】
问题2:如图2,若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,∠ECF=∠BCD,问题1的结论是否仍然成立?请说明理由.(3)、【拓展延伸】
问题3:如图3在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.32. 如图,是等边三角形,是等腰三角形,且 , , 以D为顶点作一个60°角,角的两边分别交 , 边于M,N两点,连接 , 延长至E,使 , 连接 . (1)、请在横线上写出角的度数,补充的证明过程.
(1)、请在横线上写出角的度数,补充的证明过程.证明:∵是等边三角形,∴ .
∵ , , ∴ .
∴ , .
∵ , ∴ .
即 ;
(2)、求证: .八、半角模型
-
33. 如图
 (1)、如图①,在四边形中, , , , 分别是边 , 上的点,且 . 请直接写出线段 , , 之间的数量关系:;(2)、如图②,在四边形中, , , , 分别是边 , 上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , , 分别是边 , 所在直线上的点,且 . 请画出图形(除图②外),并直接写出线段 , , 之间的数量关系.34. 已知:边长为4的正方形ABCD,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=45°,连接EF.求证:EF=BE+DF.
(1)、如图①,在四边形中, , , , 分别是边 , 上的点,且 . 请直接写出线段 , , 之间的数量关系:;(2)、如图②,在四边形中, , , , 分别是边 , 上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , , 分别是边 , 所在直线上的点,且 . 请画出图形(除图②外),并直接写出线段 , , 之间的数量关系.34. 已知:边长为4的正方形ABCD,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=45°,连接EF.求证:EF=BE+DF.思路分析:
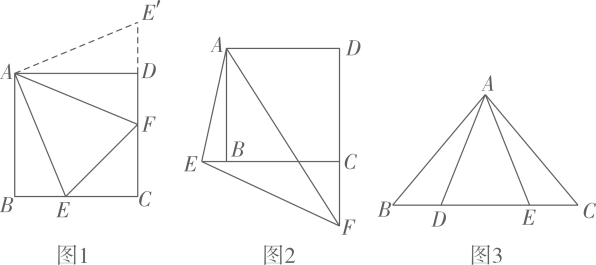 (1)、如图1,∵正方形ABCD中,AB=AD,∠BAD=∠B=∠ADC=90°,
(1)、如图1,∵正方形ABCD中,AB=AD,∠BAD=∠B=∠ADC=90°,∴把△ABE绕点A逆时针旋转90°至△ADE',则F、D、E'在一条直线上,
∠E'AF=度,……
根据定理,可证:△AEF≌△AE'F.
∴EF=BE+DF.
(2)、类比探究:
如图2,当点E在线段CB的延长线上,探究EF、BE、DF之间存在的数量关系,并写出证明过程;(3)、拓展应用:
如图3,在△ABC中,AB=AC,D、E在BC上,∠BAC=2∠DAE.若S△ABC=14,S△ADE=6,求线段BD、DE、EC围成的三角形的面积.35. 如如图,在中, . (1)、如图①,分别以 , 为边,向外作等边和等边 , 连接 , , 则(填“”“ ”或“” ;(2)、如图②,分别以 , 为腰,向内作等腰和等腰 , 且小于 , 连接 , , 猜想与的数量关系,并说明理由;(3)、如图③,以为腰向内作等腰 , 以为腰向外作等腰 , 且 , 已知点到直线的距离为3, , 求的长及点到直线的距离.36. 在正方形中,点在边上运动,点在边或上运动.
(1)、如图①,分别以 , 为边,向外作等边和等边 , 连接 , , 则(填“”“ ”或“” ;(2)、如图②,分别以 , 为腰,向内作等腰和等腰 , 且小于 , 连接 , , 猜想与的数量关系,并说明理由;(3)、如图③,以为腰向内作等腰 , 以为腰向外作等腰 , 且 , 已知点到直线的距离为3, , 求的长及点到直线的距离.36. 在正方形中,点在边上运动,点在边或上运动. (1)、若点在边上,
(1)、若点在边上,如图1,已知 , 连结 , 求证: .
如图2,已知平分 , 求证: .
(2)、若点在边上,如图 , 已知为的中点,且 , 求证: .