2023年中考数学精选真题实战测试36 三角形全等 B
试卷更新日期:2023-01-28 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
 A、4 B、8 C、12 D、162. 如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )
A、4 B、8 C、12 D、162. 如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )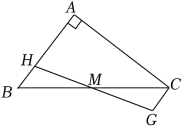 A、24 B、22 C、20 D、183. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( )
A、24 B、22 C、20 D、183. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( ) A、 B、 C、 D、4. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A、 B、 C、 D、4. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( ) A、 B、 C、 D、5. 如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )
A、 B、 C、 D、5. 如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( ) A、45° B、60° C、67.5° D、77.5°6. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
A、45° B、60° C、67.5° D、77.5°6. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )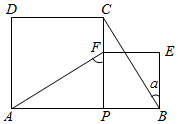 A、2α B、90°﹣α C、45°+α D、90°﹣ α7. 如图, 、 、 、 是四根长度均为5cm的火柴棒,点A、C、E共线.若 , ,则线段 的长度为( )
A、2α B、90°﹣α C、45°+α D、90°﹣ α7. 如图, 、 、 、 是四根长度均为5cm的火柴棒,点A、C、E共线.若 , ,则线段 的长度为( )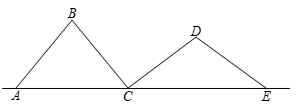 A、6 cm B、7 cm C、 D、8cm8. 如图,四边形 是菱形,点E,F分别在 边上,添加以下条件不能判定 的是( )
A、6 cm B、7 cm C、 D、8cm8. 如图,四边形 是菱形,点E,F分别在 边上,添加以下条件不能判定 的是( ) A、 B、 C、 D、9. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( )
A、 B、 C、 D、9. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( ) A、 B、 C、 D、10. 如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上, , ,则AF的长是( )
A、 B、 C、 D、10. 如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上, , ,则AF的长是( )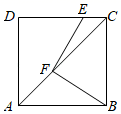 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
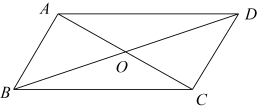
11. 如图,在四边形ABCD中,对角线AC,BD相交于点O, , 请你添加一个条件 , 使 .
 12. 如图,在边长为6的等边△ABC中,D、E分别为边BC、AC上的点,AD与BE相交于点P,若BD=CE=2,则△ABP的周长为 .
12. 如图,在边长为6的等边△ABC中,D、E分别为边BC、AC上的点,AD与BE相交于点P,若BD=CE=2,则△ABP的周长为 .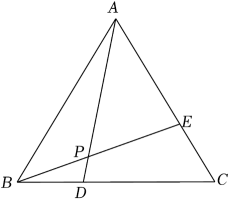 13. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
13. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等. 14. 如图,在正方形 外取一点 ,连接 , , ,过点 作 的垂线交 于点 ,若 , .下列结论:① ;② ;③点 到直线 的距离为 ;④ ,其中正确结论的序号为.
14. 如图,在正方形 外取一点 ,连接 , , ,过点 作 的垂线交 于点 ,若 , .下列结论:① ;② ;③点 到直线 的距离为 ;④ ,其中正确结论的序号为.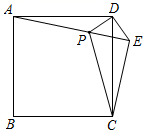 15. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.
15. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.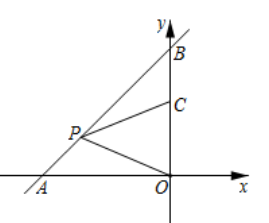 16. 如图, AB=10,点C在射线BQ上的动点,连结AC,作CD⊥AC, CD=AC ,动点E在AB 延长线上, tan∠QBE=3,连结 CE, DE ,当CE=DE, CE⊥DE时, BE 的长是 .
16. 如图, AB=10,点C在射线BQ上的动点,连结AC,作CD⊥AC, CD=AC ,动点E在AB 延长线上, tan∠QBE=3,连结 CE, DE ,当CE=DE, CE⊥DE时, BE 的长是 .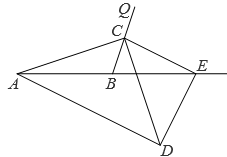
三、解答题(共8题,共72分)
-
17. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
 18. 如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F.
18. 如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F.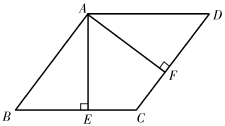 (1)、求证:△ABE≌△ADF;(2)、若AE=4,CF=2,求菱形的边长.19. 人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
(1)、求证:△ABE≌△ADF;(2)、若AE=4,CF=2,求菱形的边长.19. 人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:已知: .
求作: ,使得 ≌ .
作法:如图.
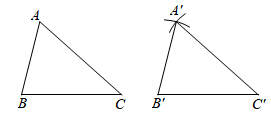
( 1 )画 ;
( 2 )分别以点 , 为圆心,线段 , 长为半径画弧,两弧相交于点 ;
( 3 )连接线段 , ,则 即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)、完成下面证明过程(将正确答案填在相应的横线上):证明:由作图可知,在 和 中,
∴ ≌_▲_.
(2)、这种作一个三角形与已知三角形全等的方法的依据是.(填序号)①AAS;②ASA;③SAS;④SSS
20. 如图,在 中,BD是它的一条对角线,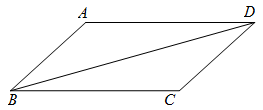 (1)、求证: ;(2)、尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);(3)、连接BE,若 ,求 的度数.21. 已知,点、、、分别在正方形的边、、、上.
(1)、求证: ;(2)、尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);(3)、连接BE,若 ,求 的度数.21. 已知,点、、、分别在正方形的边、、、上.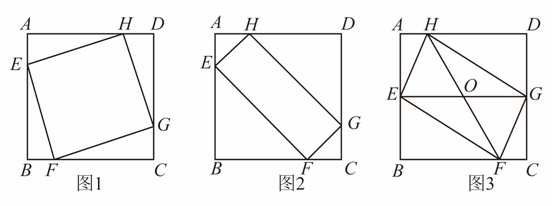 (1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.22. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
(1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.22. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.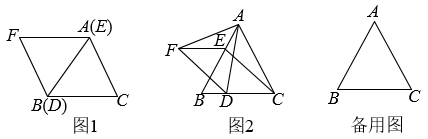 (1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.23. 和都是等边三角形.
(1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.23. 和都是等边三角形. (1)、将绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有(或)成立;请证明.(2)、将绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)、将绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.24. 在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E.
(1)、将绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有(或)成立;请证明.(2)、将绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)、将绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.24. 在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E. (1)、特例体验:如图①,若直线l∥BC,AB=AC= ,分别求出线设BD、CE和DE的长;(2)、规律探究:
(1)、特例体验:如图①,若直线l∥BC,AB=AC= ,分别求出线设BD、CE和DE的长;(2)、规律探究:(Ⅰ)如图②,若直线l从图①状态开始绕点A旋转α(0<α<45°),请探究线段BD、CE和DE的数量关系并说明理由;
(Ⅱ)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探线段BD、CE和DE的数量关系并说明理由;
(3)、尝试应用:在图③中,延长线设BD交线段AC于点F,若CE=3,DE=1,求S△BFC .