2023年中考数学精选真题实战测试35 三角形全等 A
试卷更新日期:2023-01-27 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
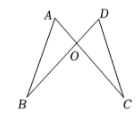 A、SSS B、SAS C、AAS D、HL2. 如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使 DOE FOE,你认为要添加的那个条件是( )
A、SSS B、SAS C、AAS D、HL2. 如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使 DOE FOE,你认为要添加的那个条件是( )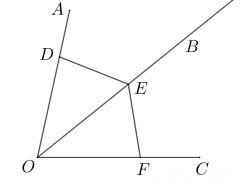 A、OD=OE B、OE=OF C、∠ODE =∠OED D、∠ODE=∠OFE3. 如图,在 中,点D,E分别是 , 边的中点,点F在 的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( )
A、OD=OE B、OE=OF C、∠ODE =∠OED D、∠ODE=∠OFE3. 如图,在 中,点D,E分别是 , 边的中点,点F在 的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( ) A、 B、 C、 D、4. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、4. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )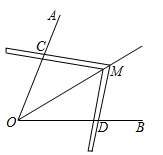 A、 B、 C、 D、5. 如图,在边长为3的正方形 中, , ,则 的长是( )
A、 B、 C、 D、5. 如图,在边长为3的正方形 中, , ,则 的长是( )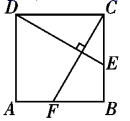 A、1 B、 C、 D、26. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O.E,F 分别为 AC,BD 上一点,且 OE=OF,连接 AF,BE,EF,若∠AFE=25°,则∠CBE 的度数为( )
A、1 B、 C、 D、26. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O.E,F 分别为 AC,BD 上一点,且 OE=OF,连接 AF,BE,EF,若∠AFE=25°,则∠CBE 的度数为( ) A、50° B、55° C、65° D、70°7. 如图,在中, , , 将绕点顺时针旋转得到 , 点A、B的对应点分别是 , , 点是边的中点,连接 , , .则下列结论错误的是( )
A、50° B、55° C、65° D、70°7. 如图,在中, , , 将绕点顺时针旋转得到 , 点A、B的对应点分别是 , , 点是边的中点,连接 , , .则下列结论错误的是( )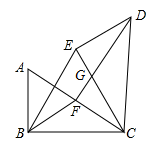 A、 B、 , C、 D、8. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
A、 B、 , C、 D、8. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
 A、①③ B、①②③ C、②③ D、①②④9. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )
A、①③ B、①②③ C、②③ D、①②④9. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )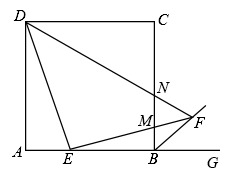 A、 B、 C、 D、110. 如图,在正方形 中, ,E为对角线 上与A,C不重合的一个动点,过点E作 于点F, 于点G,连接 .下列结论:
A、 B、 C、 D、110. 如图,在正方形 中, ,E为对角线 上与A,C不重合的一个动点,过点E作 于点F, 于点G,连接 .下列结论: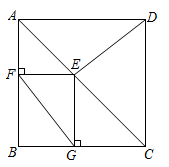
① ;② ;③ ;④ 的最小值为3.其中正确结论的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
11. 如图, , 相交于点 , , 要使≌ , 添加一个条件是 . (只写一个)
 12. 如图,在平面直角坐标系中, 为等腰三角形, ,点B到x轴的距离为4,若将 绕点O逆时针旋转 ,得到 ,则点 的坐标为.
12. 如图,在平面直角坐标系中, 为等腰三角形, ,点B到x轴的距离为4,若将 绕点O逆时针旋转 ,得到 ,则点 的坐标为. 13. 如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是.(只需写一种情况)
13. 如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是.(只需写一种情况)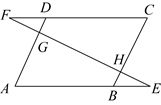 14. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).
14. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).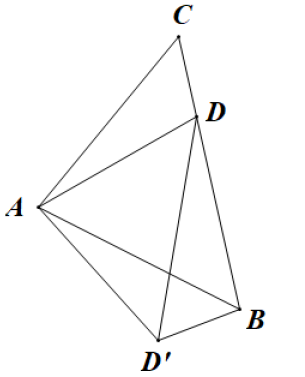 15. 三个能够重合的正六边形的位置如图.已知B点的坐标是(﹣ ,3),则A点的坐标是
15. 三个能够重合的正六边形的位置如图.已知B点的坐标是(﹣ ,3),则A点的坐标是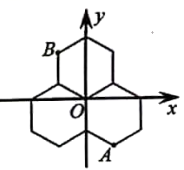 16. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.
16. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.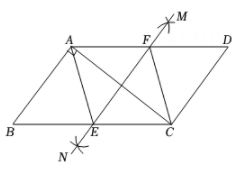
三、解答题(共8题,共72分)
-
17. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , ,求 的大小.
 18. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
18. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证: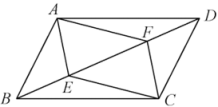 (1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.19. 如图,在平行四边形中,平分 , 平分 .
(1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.19. 如图,在平行四边形中,平分 , 平分 .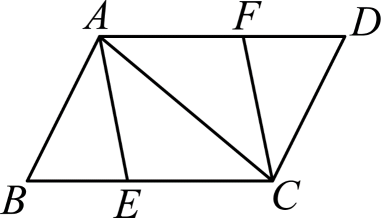 (1)、求证:;(2)、当满足什么条件时,四边形是矩形?请写出证明过程.20. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .
(1)、求证:;(2)、当满足什么条件时,四边形是矩形?请写出证明过程.20. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .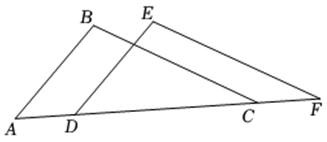 (1)、请在上述三个条件中选取一个条件,使得 ≌ .
(1)、请在上述三个条件中选取一个条件,使得 ≌ .你选取的条件为 ( 填写序号 ) ( 只需选一个条件,多选不得分 ),你判定 ≌ 的依据是 (填“ ”或“ ”或“ ”或“ ”);
(2)、利用 的结论 ≌ 求证: .21. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且. (1)、求证:;(2)、若 , , 求的长.22. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A,C重合),连接DE并延长交射线AB于点F,连接BE.
(1)、求证:;(2)、若 , , 求的长.22. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A,C重合),连接DE并延长交射线AB于点F,连接BE. (1)、求证:;(2)、求证: .23. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:
(1)、求证:;(2)、求证: .23. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
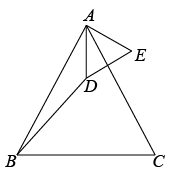
图1
(2)、解决问题:如图2,若和均为等腰直角三角形, , 点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.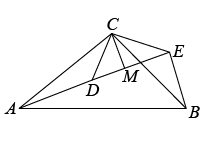
图2
24. 下面图片是八年级教科书中的一道题:如图,四边形是正方形,点是边的中点, , 且交正方形外角的平分线于点 . 求证 . (提示:取的中点 , 连接 . )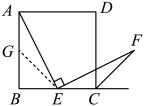 (1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;
(1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;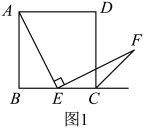 (3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.
(3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.