2023年浙教版数学七年级下册全方位训练卷第三章整式的乘除(进阶版)
试卷更新日期:2023-01-27 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,正方形卡片A类,B类和长方形卡片C类若干张,要拼一个长为(a+mb),宽为(3a+b)的大长方形(m为常数),若知道需用到的B类卡片比A类卡片少1张,则共需C类卡片( )张.
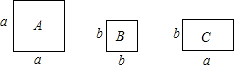 A、5 B、6 C、7 D、82. 有下列计算:
A、5 B、6 C、7 D、82. 有下列计算:① ;② ;③ ;④ ;⑤ .
其中不正确的有( )
A、1个 B、2个 C、3个 D、4个3. 已知a=833 , b=1625 , c=3219 , 则有( )A、a<b<c B、c<b<a C、c<a<b D、a<c<b4. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )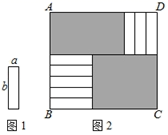 A、 B、 C、 D、5. 如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”(如 , , 则8,16均为“和谐数”),在不超过80的正整数中,所有的“和谐数”之和为( )A、430 B、440 C、450 D、4606. 已知a=2019x+2018,b=2019x+2019,c=2019x+2020.则多项式a2+b2+c2﹣ab﹣bc﹣ac的值为( )A、1 B、2 C、3 D、47. 不论x、y为什么实数,代数式x2+y2+2x﹣4y+7的值( )A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数8. 方程(x2+x﹣1)x+3=1的所有整数解的个数是( )A、5个 B、4个 C、3个 D、2个9. 观察下列各式及其展开式:( )
A、 B、 C、 D、5. 如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”(如 , , 则8,16均为“和谐数”),在不超过80的正整数中,所有的“和谐数”之和为( )A、430 B、440 C、450 D、4606. 已知a=2019x+2018,b=2019x+2019,c=2019x+2020.则多项式a2+b2+c2﹣ab﹣bc﹣ac的值为( )A、1 B、2 C、3 D、47. 不论x、y为什么实数,代数式x2+y2+2x﹣4y+7的值( )A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数8. 方程(x2+x﹣1)x+3=1的所有整数解的个数是( )A、5个 B、4个 C、3个 D、2个9. 观察下列各式及其展开式:( )……
你猜想 的展开式第三项的系数是( )
A、66 B、55 C、45 D、3610. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、二、填空题(每空3分,共21分)
-
11. 已知 = 1,则 x =()12. 计算:3(22+1)(24+1)…(232+1)﹣1,它的结果的个位数字是 .13. 已知 ,则 = .14. 南宋数学家杨辉在研究(a+b)n展开式各项的系数时,采用了特殊到一般的方法,他将(a+b)0 , (a+b)1 , (a+b)2 , (a+b)3 , …,展开后各项的系数画成如图所示的三角阵,在数学上称之为杨辉三角.已知(a+b)0=1,(a+b)1=a+b,(a+b)2=a2+2ab+b2 , (a+b)3=a3+3a2b+3ab2+b3 . 按杨辉三角写出(a+b)5的展开式是 .
 15. 如图,将长为a cm(a>2),宽为b cm(b>1)的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为cm2 . (用含a、b的代数式表示,结果要求化成最简)
15. 如图,将长为a cm(a>2),宽为b cm(b>1)的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为cm2 . (用含a、b的代数式表示,结果要求化成最简)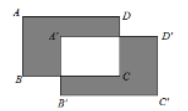 16. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2 . 若a+b=8,ab=10,则S1+S2=;当S1+S2=40时,则图3中阴影部分的面积S3=.
16. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2 . 若a+b=8,ab=10,则S1+S2=;当S1+S2=40时,则图3中阴影部分的面积S3=.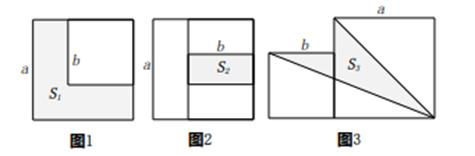
三、计算题(共3题,共16分)
-
17. 利用幂的性质计算: (结果表示为幂的形式).18. 已知 , ,(1)、求 的值;(2)、求 的值.19. 用乘法公式计算下列各式的值
(1)、(2)、(2+1)(22+1)(24+1)⋯(22n+1)四、解答题(共7题,共53分)
-
20. 先化简.再求值:(2a+b)2-2(a-2b) (2a+b)的值,其中a4=4b=16,,且ab<0·21. 已知: , ,且多项式 的值与字母y的取值无关,求 的值.22. 运用所学知识,完成下列题目.(1)、若 ,直接说出a,b,c之间的数量关系:.(2)、若 ,试确定a,b,c之间的数量关系,并说明理由;(3)、若 ,试确定a,b,c之间的数量关系,并说明理由.23. 已知 , , .(1)、当 , 时, , .(2)、当 , 时, , .(3)、观察(1)和(2)的结果,可以得出结论: (n为正整数).(4)、此性质可以用来进行积的乘方运算,反之仍然成立.如 , ,….应用上述等式,求 的值.24. 有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙 .
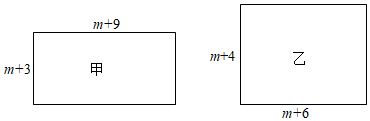 (1)、①计算:S甲= , S乙=;
(1)、①计算:S甲= , S乙=;②用“<”,“=”或“>”填空:S甲S乙 .
(2)、若一个正方形纸片的周长与乙长方形的周长相等,面积为S正 .①该正方形的边长是 ▲ 用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否符合题意,并通过计算说明你的理由.
25. 好学小东同学,在学习多项式乘以多项式时发现:( x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为: x•2x•3x=3x3 , 常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是: ×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x .请你认真领会小东同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)、计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为 .(2)、( x+6)(2x+3)(5x-4)所得多项式的二次项系数为 .(3)、若计算(x2+x+1)(x2-3x+a)(2x-1)所得多项式不含一次项,求a的值;(4)、若(x+1)2021=a0x2021+a1x2020+a2x2019+···+a2020x+a2021 , 则a2020= .26. 【阅读材料】“数形结合”是一种非常重要的数学思想方法.比如:在学习“整式的乘法”时,我们通过构造几何图形,用“等积法”直观地推导出了完全平方和公式:(如图1).利用“数形结合”的思想方法,可以从代数角度解决图形问题,也可以用图形关系解决代数问题.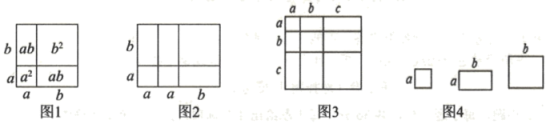 (1)、【方法应用】根据以上材料提供的方法,完成下列问题:
(1)、【方法应用】根据以上材料提供的方法,完成下列问题:由图2可得等式:;由图3可得等式:;
(2)、利用图3得到的结论,解决问题:若 , , 则;(3)、如图4,若用其中张边长为的正方形,张边长为的正方形,张边长分别为、的长方形纸片拼出一个面积为长方形(无空隙、无重叠地拼接),则;(4)、如图4,若有3张边长为的正方形纸片,4张边长分别为的长方形纸片,5张边长为的正方形纸片.从中取出若干张纸片,每种纸片至少取一张.把取出的这些纸片拼成一个正方形(无空隙、无重叠地拼接),则拼成的正方形的边长最长可以为 .(5)、【方法拓展】已知正数 , , 和 , , , 满足 . 试通过构造边长为的正方形,利用图形面积来说明 .