2023年中考数学精选真题实战测试34 直角三角形与勾股定理 B
试卷更新日期:2023-01-26 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
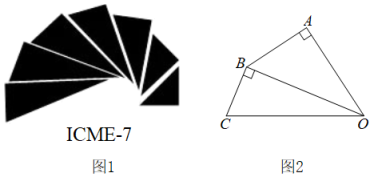 A、 B、 C、 D、12. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
A、 B、 C、 D、12. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )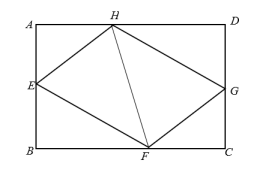 A、 B、 C、 D、3. 如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE, , ,则 ( )
A、 B、 C、 D、3. 如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE, , ,则 ( )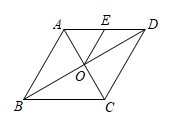 A、4 B、 C、2 D、4. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )
A、4 B、 C、2 D、4. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )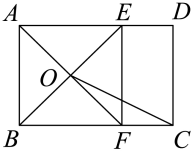 A、 B、 C、 D、5. 已知直线 与 轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )A、(1,1) B、(1,1)或(1,2) C、(1,1)或(1,2)或(2,1) D、(0,0)或(1,1)或(1,2)或(2,1)6. 将一副直角三角板按如图所示的方式放置,使用 角的三角板的直角边和含 角的三角板的直角边垂直,则∠1的度数为( )
A、 B、 C、 D、5. 已知直线 与 轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )A、(1,1) B、(1,1)或(1,2) C、(1,1)或(1,2)或(2,1) D、(0,0)或(1,1)或(1,2)或(2,1)6. 将一副直角三角板按如图所示的方式放置,使用 角的三角板的直角边和含 角的三角板的直角边垂直,则∠1的度数为( ) A、 B、 C、 D、7. 如图,在边长为3的正方形 中, , ,则 的长是( )
A、 B、 C、 D、7. 如图,在边长为3的正方形 中, , ,则 的长是( )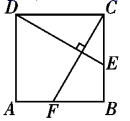 A、1 B、 C、 D、28. 如图,在中, , D是AB的中点,延长CB至点E,使 , 连接DE,F为DE中点,连接BF.若 , , 则BF的长为( )
A、1 B、 C、 D、28. 如图,在中, , D是AB的中点,延长CB至点E,使 , 连接DE,F为DE中点,连接BF.若 , , 则BF的长为( )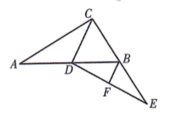 A、5 B、4 C、6 D、89. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:
A、5 B、4 C、6 D、89. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:①;②;③;④.其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个10. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )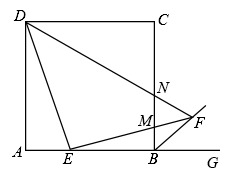 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题(每空3分,共18分)
-
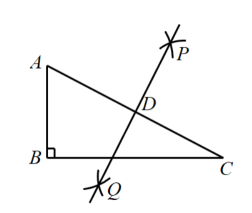
11. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .
 12. 如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是 .
12. 如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是 .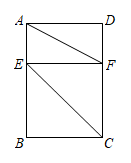 13. 如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.
13. 如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.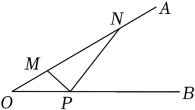 14. 如图,把一张矩形纸片沿对角线折叠,若BC=9,CD=3,那么阴影部分的面积为 .
14. 如图,把一张矩形纸片沿对角线折叠,若BC=9,CD=3,那么阴影部分的面积为 .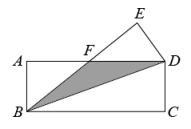 15. 如图,菱形 中,对角线 与 相交于点 ,若 , ,则 的长为cm.
15. 如图,菱形 中,对角线 与 相交于点 ,若 , ,则 的长为cm.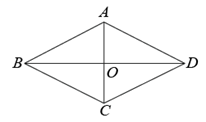 16. 如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且 , 连接EF交边AD于点G.过点A作 , 垂足为点M,交边CD于点N.若 , , 则线段AN的长为
16. 如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且 , 连接EF交边AD于点G.过点A作 , 垂足为点M,交边CD于点N.若 , , 则线段AN的长为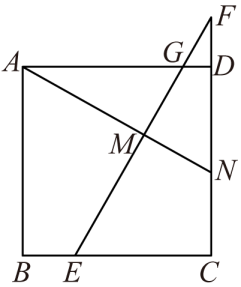
三、解答题(共7题,共72分)
-
17. 如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:
 (1)、°;(2)、若 , , 则 .18. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .
(1)、°;(2)、若 , , 则 .18. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .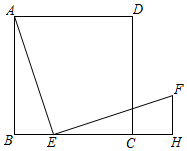 (1)、求证: ;(2)、若 , ,用x表示DF的长.19. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且.
(1)、求证: ;(2)、若 , ,用x表示DF的长.19. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且. (1)、求证:;(2)、若 , , 求的长.20. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,
(1)、求证:;(2)、若 , , 求的长.20. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF, (1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.21. 同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.21. 同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答: (1)、【问题一】如图①,正方形的对角线相交于点 , 点又是正方形的一个顶点,交于点 , 交于点 , 则与的数量关系为;(2)、【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心 , 直线分别与、交于点、 , 直线分别与、交于点、 , 且 , 若正方形边长为8,求四边形的面积;
(1)、【问题一】如图①,正方形的对角线相交于点 , 点又是正方形的一个顶点,交于点 , 交于点 , 则与的数量关系为;(2)、【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心 , 直线分别与、交于点、 , 直线分别与、交于点、 , 且 , 若正方形边长为8,求四边形的面积; (3)、【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且 , . 在直线上是否存在点 , 使为直角三角形?若存在,求出的长度;若不存在,说明理由.
(3)、【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且 , . 在直线上是否存在点 , 使为直角三角形?若存在,求出的长度;若不存在,说明理由.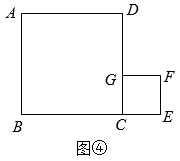 22. 已知是的角平分线,点E,F分别在边 , 上, , , 与的面积之和为S.
22. 已知是的角平分线,点E,F分别在边 , 上, , , 与的面积之和为S. (1)、填空:当 , , 时,
(1)、填空:当 , , 时,①如图1,若 , , 则 , ;
②如图2,若 , , 则 , ;
(2)、如图3,当时,探究S与m、n的数量关系,并说明理由:(3)、如图4,当 , , , 时,请直接写出S的大小.23. 综合与实践 (1)、知识再现
(1)、知识再现
如图 , 中, , 分别以、、为边向外作的正方形的面积为、、 . 当 , 时, .(2)、问题探究如图,中, .
如图 , 分别以、、为边向外作的等腰直角三角形的面积为、、 , 则、、之间的数量关系是 .(3)、如图 , 分别以、、为边向外作的等边三角形的面积为、、 , 试猜想、、之间的数量关系,并说明理由.(4)、实践应用
如图4,将图中的绕点逆时针旋转一定角度至 , 绕点顺时针旋转一定角度至 , 、相交于点 . 求证:;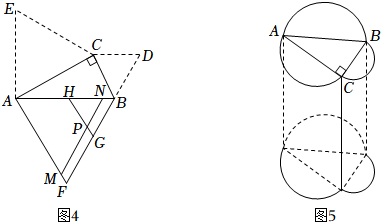 (5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.
(5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.