2023年中考数学精选真题实战测试33 直角三角形与勾股定理 A
试卷更新日期:2023-01-26 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
 A、 B、 C、 D、2. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( )
A、 B、 C、 D、2. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( ) A、2 B、 C、 D、3. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
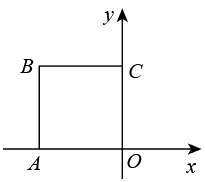
A、2 B、 C、 D、3. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、4. 如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为 , 则图象最低点E的坐标为( )
A、 B、 C、 D、4. 如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为 , 则图象最低点E的坐标为( )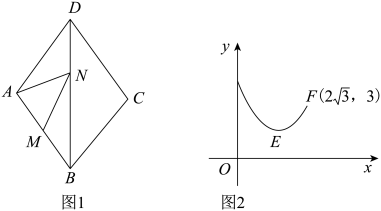 A、 B、 C、 D、5. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、 B、 C、 D、5. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、6. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( )
A、 B、 C、 D、6. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( ) A、25π+24 B、5π+24 C、25π D、5π7. 如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若 , , 则点B到的距离为( )
A、25π+24 B、5π+24 C、25π D、5π7. 如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若 , , 则点B到的距离为( )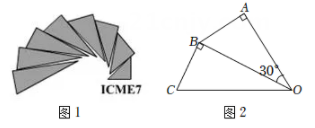 A、 B、 C、1 D、28. 如图,在中, , 将绕点C顺时针旋转得到 , 其中点与点A是对应点,点与点B是对应点.若点恰好落在边上,则点A到直线的距离等于( )
A、 B、 C、1 D、28. 如图,在中, , 将绕点C顺时针旋转得到 , 其中点与点A是对应点,点与点B是对应点.若点恰好落在边上,则点A到直线的距离等于( ) A、 B、 C、3 D、29. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( )
A、 B、 C、3 D、29. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每空3分,共18分)
-
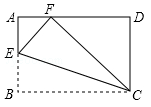
11. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
 12. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 .
12. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 . 13. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
13. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .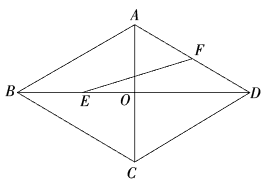 14. 小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
14. 小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .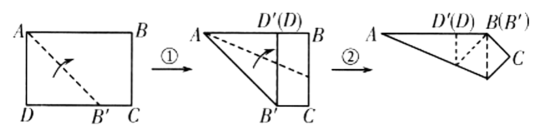 15. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
15. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .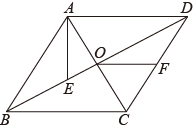 16. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .
16. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .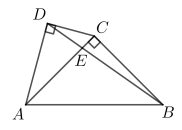
三、解答题(共8题,共72分)
-
17. 如图,在和中, , , , 且点D在线段上,连 .
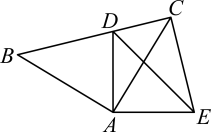 (1)、求证:;(2)、若 , 求的度数.18. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .
(1)、求证:;(2)、若 , 求的度数.18. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .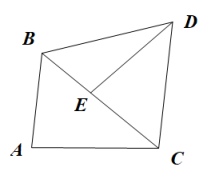 (1)、求证:;(2)、若 , 求的面积.19. 如图,在中, , , 是边上的一点,以为直角边作等腰 , 其中 , 连接 .
(1)、求证:;(2)、若 , 求的面积.19. 如图,在中, , , 是边上的一点,以为直角边作等腰 , 其中 , 连接 . (1)、求证:;(2)、若时,求的长.20. 如图,在矩形ABCD中,E为AB的中点,连接CE并延长,交DA的延长线于点F.
(1)、求证:;(2)、若时,求的长.20. 如图,在矩形ABCD中,E为AB的中点,连接CE并延长,交DA的延长线于点F. (1)、求证:△AEF≌△BEC.(2)、若CD=4,∠F=30°,求CF的长.21. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:
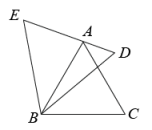
(1)、求证:△AEF≌△BEC.(2)、若CD=4,∠F=30°,求CF的长.21. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
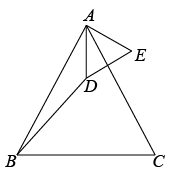
图1
(2)、解决问题:如图2,若和均为等腰直角三角形, , 点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.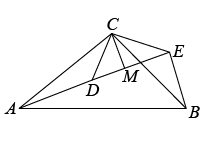
图2
22. 下面图片是八年级教科书中的一道题:如图,四边形是正方形,点是边的中点, , 且交正方形外角的平分线于点 . 求证 . (提示:取的中点 , 连接 . )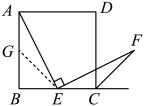 (1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;
(1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;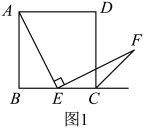 (3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.23. 阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:
(3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.23. 阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:如图,和都是等边三角形,点在上.
求证:以、、为边的三角形是钝角三角形.
(1)、【探究发现】小明通过探究发现:连接 , 根据已知条件,可以证明 , , 从而得出为钝角三角形,故以、、为边的三角形是钝角三角形.请你根据小明的思路,写出完整的证明过程.
(2)、【拓展迁移】如图,四边形和四边形都是正方形,点在上.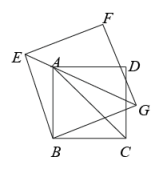
①试猜想:以、、为边的三角形的形状,并说明理由.
②若 , 试求出正方形的面积.
24. 【经典回顾】梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中, , 四边形、和分别是以的三边为一边的正方形.延长和 , 交于点 , 连接并延长交于点 , 交于点 , 延长交于点 .
(1)、证明:;(2)、证明:正方形的面积等于四边形的面积;(3)、请利用(2)中的结论证明勾股定理.(4)、【迁移拓展】如图2,四边形和分别是以的两边为一边的平行四边形,探索在下方是否存在平行四边形 , 使得该平行四边形的面积等于平行四边形、的面积之和.若存在,作出满足条件的平行四边形(保留适当的作图痕迹);若不存在,请说明理由.