2023年浙教版数学七年级下册全方位训练卷3.4乘法公式
试卷更新日期:2023-01-25 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列多项式乘以多项式中,能用平方差公式计算的是( )A、 B、 C、 D、2. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形;验证了一个等式,则这个等式是( )
 A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣ab=a(a﹣b)3. 我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式a2−b2=(a+b)(a−b)的是( )A、
A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣ab=a(a﹣b)3. 我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式a2−b2=(a+b)(a−b)的是( )A、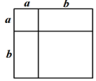 B、
B、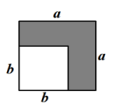 C、
C、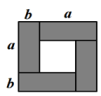 D、
D、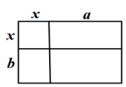 4. 某同学粗心大意,分解因式时,把式子中的一部分弄污了,那么你认为式子中的所对应的代数式是( )A、 B、 C、 D、5. 将边长分别为和a-b的两个正方形摆放成如图所示的位置,则阴影部分的面积化简后的结果( )
4. 某同学粗心大意,分解因式时,把式子中的一部分弄污了,那么你认为式子中的所对应的代数式是( )A、 B、 C、 D、5. 将边长分别为和a-b的两个正方形摆放成如图所示的位置,则阴影部分的面积化简后的结果( ) A、 B、 C、2ab D、4ab6. 如图,用不同的代数式表示图中阴影部分的面积,可得等式( )
A、 B、 C、2ab D、4ab6. 如图,用不同的代数式表示图中阴影部分的面积,可得等式( )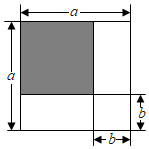 A、(a+b)2=a2+2ab+b2 B、(a﹣b)2=a2+2ab﹣b2 C、(a+b)(a﹣b)=a2﹣b2 D、(a﹣b)2=a2﹣2ab+b27. 有两个正方形 ,现将 放在 的内部得图甲,将 并列放置后构造新的正方形得图乙,若图甲和图乙中阴影部分的面积分别为3和16,则正方形 的面积之和为 ( )
A、(a+b)2=a2+2ab+b2 B、(a﹣b)2=a2+2ab﹣b2 C、(a+b)(a﹣b)=a2﹣b2 D、(a﹣b)2=a2﹣2ab+b27. 有两个正方形 ,现将 放在 的内部得图甲,将 并列放置后构造新的正方形得图乙,若图甲和图乙中阴影部分的面积分别为3和16,则正方形 的面积之和为 ( ) A、13 B、11 C、19 D、218. 今年各地疫情时有出现,为了不影响学习,学校组织同学们进行网上学习,课堂上老师布置了四个运算题目,小刚给出了四个题的答案:
A、13 B、11 C、19 D、218. 今年各地疫情时有出现,为了不影响学习,学校组织同学们进行网上学习,课堂上老师布置了四个运算题目,小刚给出了四个题的答案:计算:
① ;② ;③ ; ④
则小刚做对的题数是( )
A、0个 B、1个 C、2个 D、3个9. 若 , , 则( )A、-3 B、3 C、-4 D、410. 在多项式添加一个单项式,使得到的多项式能运用完全平方公式分解因式,则下列表述正确的是( )嘉琪:添加 ,
陌陌:添加 ,
嘟嘟:添加 ,
A、嘉琪和陌陌的做法正确 B、嘉琪和嘟嘟的做法正确 C、陌陌和嘟嘟的做法正确 D、三位同学的做法都错误二、填空题(每题4分,共24分)
-
11. 已知 , .12. 计算: .13. 如图,在边长为a(cm)的大正方形内放入三个边长都为b(cm)(a>b)的小正方形纸片,这三张纸片没有盖住的面积是4cm2 , 则a2-2ab+b2的值为.
 14. 已知 , 则的值为 .15. 计算:16. 若 , 则的值为 .
14. 已知 , 则的值为 .15. 计算:16. 若 , 则的值为 .三、计算题(共2题,共20分)
-
17. 运用整式乘法公式进行计算(1)、(50)2(2)、1232-122×118.18. 要求:利用乘法公式计算(1)、(2)、
四、解答题(共7题,共46分)
-
19. 先化简,再求值: ,其中 .20. 已知 , 求的值.21. 证明是13的倍数.22. 将多项式 加上一个整式后,使它能成为另一个整式的平方,你有哪些方法,请写出三类不同的解法.23. 已知 , ,(1)、求代数式的值;(2)、求代数式的值.24. 【背景知识】用两种方法计算同一个图形的面积,就可以得到一个等式.例如:图1是一个边长为的正方形,从整体来看,它的面积可以表示为 , 从分块来看,这个正方形有四块,其中面积为的正方形有1块,面积为的正方形有1块,面积为ab的长方形有2块,因此,该正方形的面积还可以表示为 , 这两种方法都是求同一个正方形的面积,于是得到 .


 (1)、【能力提升】请你根据背景知识和图2推导等式;(2)、【能力提升】请你根据背景知识和图3推导等式;(3)、【拓展应用】若 , , 利用(2)得到的结论,求图3中阴影部分的面积.25. 完全平方公式进行适当的变形后,可以解决很多的数学问题.
(1)、【能力提升】请你根据背景知识和图2推导等式;(2)、【能力提升】请你根据背景知识和图3推导等式;(3)、【拓展应用】若 , , 利用(2)得到的结论,求图3中阴影部分的面积.25. 完全平方公式进行适当的变形后,可以解决很多的数学问题.如:若x满足 , 求的值.
解题思路:由得 ,
可设 , , 则 , ,
∴;
(1)、请仿照上面的方法求解下面问题:①若x满足 , 求的值;
②若x满足 , 求的值;
(2)、应用上面的解题思路解决问题:如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分的面积.