2023年中考数学精选真题实战测试30 平行线与相交线 B
试卷更新日期:2023-01-24 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图, , , 则的度数是( )
 A、137° B、53° C、47° D、43°2. 如图,已知 , 于点 , 若 , 则的度数是( )
A、137° B、53° C、47° D、43°2. 如图,已知 , 于点 , 若 , 则的度数是( ) A、 B、 C、 D、3. 如图,.若 , 则的大小为( )
A、 B、 C、 D、3. 如图,.若 , 则的大小为( )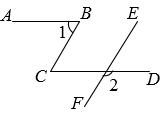 A、 B、 C、 D、4. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( )
A、 B、 C、 D、4. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( ) A、 B、 C、 D、5. 如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,过点A作AC⊥l2 , 垂足为C,若∠1=52°,则∠2的度数是( )
A、 B、 C、 D、5. 如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,过点A作AC⊥l2 , 垂足为C,若∠1=52°,则∠2的度数是( ) A、32° B、38° C、48° D、52°6. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )
A、32° B、38° C、48° D、52°6. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )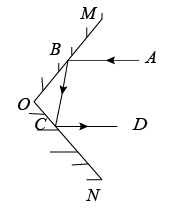 A、 B、 C、 D、7. 如图, , 则的度数是( )
A、 B、 C、 D、7. 如图, , 则的度数是( )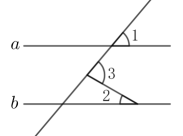 A、 B、 C、 D、8. 如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A、 B、 C、 D、8. 如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )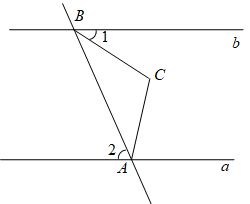 A、57° B、63° C、67° D、73°9. 要得知作业纸上两相交直线AB , CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案Ⅰ、Ⅱ,说法正确的是( )
A、57° B、63° C、67° D、73°9. 要得知作业纸上两相交直线AB , CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案Ⅰ、Ⅱ,说法正确的是( )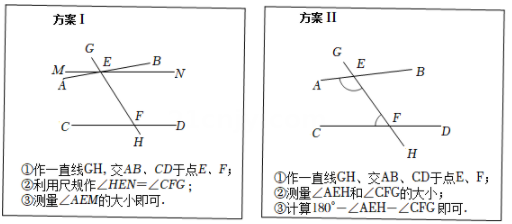 A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行10. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )
A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行10. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )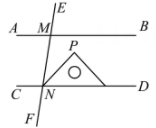 A、15° B、25° C、35° D、45°
A、15° B、25° C、35° D、45°二、填空题(每空3分,共18分)
-
11. 一副三角板如图放置, , , , 则 .
 12. 将一副直角三角板如图放置,已知 , , , 则°.
12. 将一副直角三角板如图放置,已知 , , , 则°.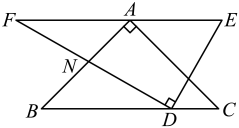 13. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 .
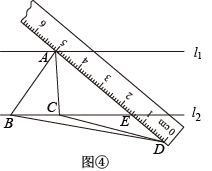
13. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 . 14. 如图,在△ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为 .
14. 如图,在△ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为 . 15. 如图,在菱形 中, , 为 中点,点 在 延长线上, 、 分别为 、 中点, , ,则 .
15. 如图,在菱形 中, , 为 中点,点 在 延长线上, 、 分别为 、 中点, , ,则 .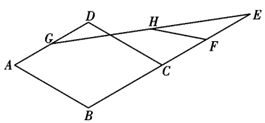 16. 一副三角板如图所示摆放,且 ,则 的度数为 .
16. 一副三角板如图所示摆放,且 ,则 的度数为 .

三、解答题(共8题,共72分)
-
17. 如图, BD 是 △ABC的角平分线, DE∥BC ,交 AB 于点E.
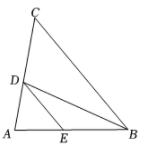 (1)、求证: .(2)、当AB=AC时,请判断 CD 与ED的大小关系,并说明理由.18. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .
(1)、求证: .(2)、当AB=AC时,请判断 CD 与ED的大小关系,并说明理由.18. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .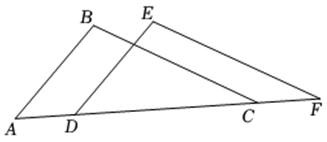 (1)、请在上述三个条件中选取一个条件,使得 ≌ .
(1)、请在上述三个条件中选取一个条件,使得 ≌ .你选取的条件为 ( 填写序号 ) ( 只需选一个条件,多选不得分 ),你判定 ≌ 的依据是 (填“ ”或“ ”或“ ”或“ ”);
(2)、利用 的结论 ≌ 求证: .19. 如图,在四边形中, , .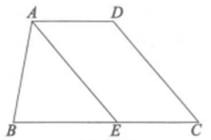 (1)、求的度数;(2)、平分交于点 , .求证:.20. 如图,在 中, 为 的外角.
(1)、求的度数;(2)、平分交于点 , .求证:.20. 如图,在 中, 为 的外角. (1)、尺规作图:作 的平分线 (保留作图痕迹可加黑,不写作法);(2)、若 ,在(1)的条件下,求证: .21. 如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.
(1)、尺规作图:作 的平分线 (保留作图痕迹可加黑,不写作法);(2)、若 ,在(1)的条件下,求证: .21. 如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B. (1)、利用尺规作∠NAB的平分线与PQ交于点C;(2)、若∠ABP=70°,求∠ACB的度数.22. 已知, 和 中, , .试探究:
(1)、利用尺规作∠NAB的平分线与PQ交于点C;(2)、若∠ABP=70°,求∠ACB的度数.22. 已知, 和 中, , .试探究: (1)、如图1, 与 的关系是;(2)、如图2,写出 与 的关系,并说明理由;(3)、根据上述探究,请归纳得到一个真命题.23. 某兴趣小组通过探究圆的基本知识,找到了借助圆作“过直线外一点作已知直线的平行线”的方法,如图,过点C作直线l的平行线.作图过程如下:
(1)、如图1, 与 的关系是;(2)、如图2,写出 与 的关系,并说明理由;(3)、根据上述探究,请归纳得到一个真命题.23. 某兴趣小组通过探究圆的基本知识,找到了借助圆作“过直线外一点作已知直线的平行线”的方法,如图,过点C作直线l的平行线.作图过程如下: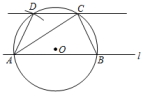
第一步:在直线l上任意取两点A,B,连接AC,BC,且AC>BC;
第二步:作△ABC的外接圆O;
第三步:以点A为圆心,CB长为半径作弧,交于点D,连接AD;
第四步:作直线CD,则直线CD即为所求作的平行线.
(1)、为了说明这一方法的正确性,需要对其进行证明如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图,△ABC内接于⊙O,AC>BC,D为弧AC上一点,且满足.求证:.
(2)、聪聪认为,在△ABC中,若AC=BC,过点C作直线l的平行线 , 则为⊙O的切线,你认为聪聪的想法正确吗?请说明理由.24. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线 , 与的面积相等吗?为什么?
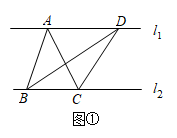
解:相等.理由如下:
设与之间的距离为 , 则 , .
∴ .
【探究】
(1)、如图②,当点在 , 之间时,设点 , 到直线的距离分别为 , , 则 .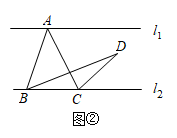
证明:∵ ▲
▲
▲
(2)、如图③,当点在 , 之间时,连接并延长交于点 , 则 .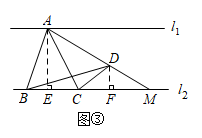
证明:过点作 , 垂足为 , 过点作 , 垂足为 , 则 ,
∴ ▲ .
∴ ▲ .
∴ .
由【探究】(1)可知 ▲ ,
∴ .
(3)、如图④,当点在下方时,连接交于点 . 若点 , , 所对应的刻度值分别为5,1.5,0,的值为 .