2023年中考数学精选真题实战测试29 平行线与相交线 A
试卷更新日期:2023-01-24 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,直线 ,直线c与直线a,b分别相交于点A,B, ,垂足为C.若 ,则 ( )
 A、52° B、45° C、38° D、26°2. 数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A、52° B、45° C、38° D、26°2. 数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( ) A、同旁内角、同位角、内错角 B、同位角、内错角、对顶角 C、对顶角、同位角、同旁内角 D、同位角、内错角、同旁内角3. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( )
A、同旁内角、同位角、内错角 B、同位角、内错角、对顶角 C、对顶角、同位角、同旁内角 D、同位角、内错角、同旁内角3. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( ) A、40° B、60° C、80° D、100°4. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A、40° B、60° C、80° D、100°4. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( ) A、10° B、15° C、20° D、30°5. 如图, , 则的度数为( )
A、10° B、15° C、20° D、30°5. 如图, , 则的度数为( ) A、 B、 C、 D、6. 如图,直线 , 直线分别交于点 , 点在直线上, , 若 , 则的度数是( )
A、 B、 C、 D、6. 如图,直线 , 直线分别交于点 , 点在直线上, , 若 , 则的度数是( ) A、 B、 C、 D、7. 如图,是一块直角三角板,其中 . 直尺的一边DE经过顶点A,若 , 则的度数为( )
A、 B、 C、 D、7. 如图,是一块直角三角板,其中 . 直尺的一边DE经过顶点A,若 , 则的度数为( )
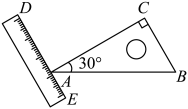 A、100° B、120° C、135° D、150°8. 小明将一块直角三角板摆放在直尺上,如图所示,则与的关系是( )
A、100° B、120° C、135° D、150°8. 小明将一块直角三角板摆放在直尺上,如图所示,则与的关系是( )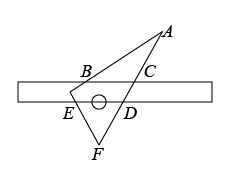 A、互余 B、互补 C、同位角 D、同旁内角9. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )
A、互余 B、互补 C、同位角 D、同旁内角9. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )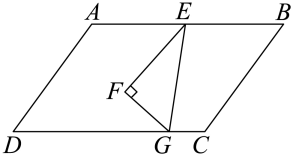 A、100° B、80° C、70° D、60°10. 如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线l与出射光线m平行.若入射光线l与镜面的夹角 , 则的度数为( )
A、100° B、80° C、70° D、60°10. 如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线l与出射光线m平行.若入射光线l与镜面的夹角 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 如图,已知 , , 则的度数为.
 12. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .
12. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .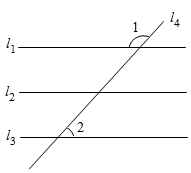 13. 两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE与AC交于M,若 , 则∠DMC的大小为 .
13. 两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE与AC交于M,若 , 则∠DMC的大小为 .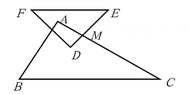 14. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 .
14. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 . 15. 如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.
15. 如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.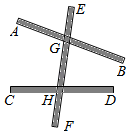 16. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 、 ,若 , ,则 的度数是.
16. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 、 ,若 , ,则 的度数是.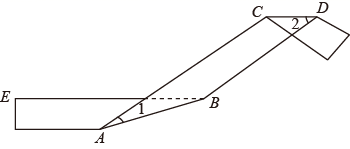
三、解答题(共8题,共72分)
-
17. 如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
 18. 图1是光伏发电场景,其示意图如图2,EF为吸热塔,在地平线EG上的点B,B'处各安装定日镜(介绍见图3).绕各中心点(A,A')旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1m,EB=8m,EB'=8 m,在点A观测点F的仰角为45°
18. 图1是光伏发电场景,其示意图如图2,EF为吸热塔,在地平线EG上的点B,B'处各安装定日镜(介绍见图3).绕各中心点(A,A')旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1m,EB=8m,EB'=8 m,在点A观测点F的仰角为45°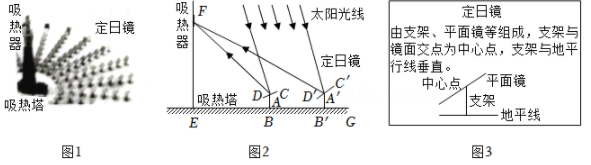 (1)、点F的高度EF为m.(2)、设∠DAB=α,∠D'A'B'=β,则α与β的数量关系是.19. 如图
(1)、点F的高度EF为m.(2)、设∠DAB=α,∠D'A'B'=β,则α与β的数量关系是.19. 如图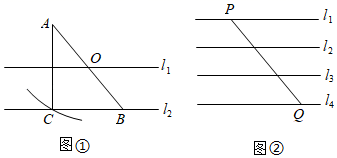 (1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)20. 如图,B、F、C、E是直线l上的四点, .
(1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)20. 如图,B、F、C、E是直线l上的四点, . (1)、求证: ;(2)、将 沿直线l翻折得到 .
(1)、求证: ;(2)、将 沿直线l翻折得到 .①用直尺和圆规在图中作出 (保留作图痕迹,不要求写作法);
②连接 ,则直线 与l的位置关系是▲ .
21. 如图,点 是 的边 上的动点, ,连接 ,并将线段 绕点 逆时针旋转 得到线段 .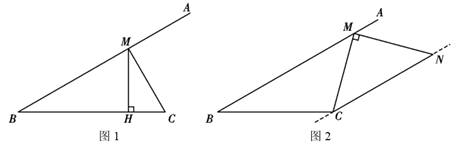 (1)、如图1,作 ,垂足 在线段 上,当 时,判断点 是否在直线 上,并说明理由;(2)、如图2,若 , ,求以 、 为邻边的正方形的面积 .22. 有一组对边平行,一个内角是它对角的两倍的四边形叫做倍角梯形.
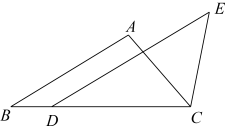
(1)、如图1,作 ,垂足 在线段 上,当 时,判断点 是否在直线 上,并说明理由;(2)、如图2,若 , ,求以 、 为邻边的正方形的面积 .22. 有一组对边平行,一个内角是它对角的两倍的四边形叫做倍角梯形. (1)、已知四边形ABCD是倍角梯形,AD∥BC,∠A=100°,请直接写出所有满足条件的∠D的度数;(2)、如图1,在四边形ABCD中,∠BAD+∠B=180°,BC=AD+CD.求证:四边形ABCD是倍角梯形;(3)、如图2,在(2)的条件下,连结AC,当AB=AC=AD=2时,求BC的长.
(1)、已知四边形ABCD是倍角梯形,AD∥BC,∠A=100°,请直接写出所有满足条件的∠D的度数;(2)、如图1,在四边形ABCD中,∠BAD+∠B=180°,BC=AD+CD.求证:四边形ABCD是倍角梯形;(3)、如图2,在(2)的条件下,连结AC,当AB=AC=AD=2时,求BC的长.


