2023年中考数学精选真题实战测试28 图形的基础知识 B
试卷更新日期:2023-01-24 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
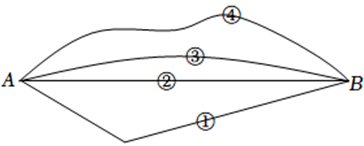 A、① B、② C、③ D、④2. 下列图形中,为圆柱的侧面展开图的是( )A、
A、① B、② C、③ D、④2. 下列图形中,为圆柱的侧面展开图的是( )A、 B、
B、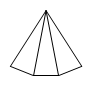 C、
C、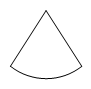 D、
D、 3. 如图,直线AB与CD相交于点O, , ,则 的度数是( )
3. 如图,直线AB与CD相交于点O, , ,则 的度数是( ) A、25° B、30° C、40° D、50°4. 两个矩形的位置如图所示,若 , 则( )
A、25° B、30° C、40° D、50°4. 两个矩形的位置如图所示,若 , 则( )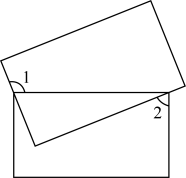 A、 B、 C、 D、5. 若 ,则 的余角的大小是( )A、50° B、60° C、140° D、160°6. 如图,将矩形绕着它的一边所在的直线1旋转一周,可以得到的立体图形是( )
A、 B、 C、 D、5. 若 ,则 的余角的大小是( )A、50° B、60° C、140° D、160°6. 如图,将矩形绕着它的一边所在的直线1旋转一周,可以得到的立体图形是( ) A、
A、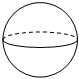 B、
B、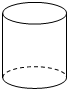 C、
C、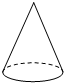 D、
D、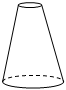 7. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“亮”字所在面相对的面上的汉字是( )
7. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“亮”字所在面相对的面上的汉字是( )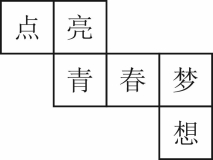 A、青 B、春 C、梦 D、想8. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或39. 如图,将一副三角尺按下列位置摆放,使 和 互余的摆放方式是( )A、
A、青 B、春 C、梦 D、想8. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或39. 如图,将一副三角尺按下列位置摆放,使 和 互余的摆放方式是( )A、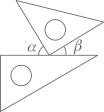 B、
B、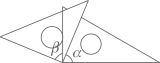 C、
C、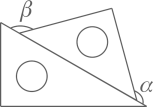 D、
D、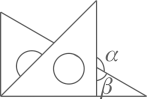 10. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为( )
10. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为( )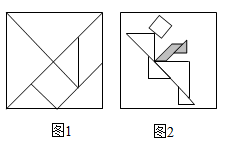 A、3 B、 C、2 D、
A、3 B、 C、2 D、二、填空题(每空3分,共18分)
-
11. 如图,点C是线段AB的中点,若AC=2cm,则AB=cm.
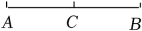 12. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .
12. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .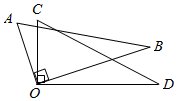 13. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
13. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .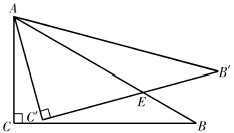 14. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).15. 如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD=度.
14. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).15. 如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD=度.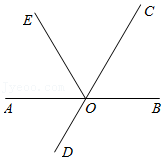 16. 如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是.
16. 如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是.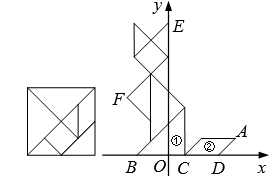
三、解答题(共8题,共72分)
-
17. 如图,数轴上从左到右有点A,B,C,D,其中点C为原点,A,D所对应的数分别为-5,1,点B为AD的中点.
 (1)、在图中标出点C的位置,并直写出点B对应的数;(2)、若在数轴上另取一点E,且B,E两点间的距离是7,求A,B,C,D,E对应的数的和.18. 如图,在 中, ,
(1)、在图中标出点C的位置,并直写出点B对应的数;(2)、若在数轴上另取一点E,且B,E两点间的距离是7,求A,B,C,D,E对应的数的和.18. 如图,在 中, ,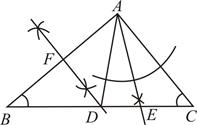 (1)、通过观察尺规作图的痕迹,可以发现直线 是线段 的 , 射线 是 的;(2)、在(1)所作的图中,求 的度数.19. A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a-b,B、C两站之间的距离BC=2a-b,B、D两站之间的距离BD=a-2b-1.求:
(1)、通过观察尺规作图的痕迹,可以发现直线 是线段 的 , 射线 是 的;(2)、在(1)所作的图中,求 的度数.19. A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a-b,B、C两站之间的距离BC=2a-b,B、D两站之间的距离BD=a-2b-1.求: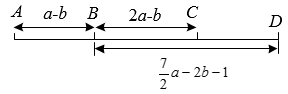 (1)、A、C两站之间的距离AC;(2)、若A、C两站之间的距离AC=90km,求C、D两站之间的距离CD.20. 如图,是菱形的对角线, .
(1)、A、C两站之间的距离AC;(2)、若A、C两站之间的距离AC=90km,求C、D两站之间的距离CD.20. 如图,是菱形的对角线, .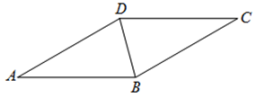 (1)、请用直尺和圆规,在上找点F,使(不要求写作法,保留作图痕迹);(2)、在(1)的条件下,连接 , 求的度数.21. 如图,已知点 、 在 的边 上, , .
(1)、请用直尺和圆规,在上找点F,使(不要求写作法,保留作图痕迹);(2)、在(1)的条件下,连接 , 求的度数.21. 如图,已知点 、 在 的边 上, , . (1)、求证: ;(2)、若 ,求 的度数.22. 如图,在 中, 平分 , 是 边上的一点,连接 , .
(1)、求证: ;(2)、若 ,求 的度数.22. 如图,在 中, 平分 , 是 边上的一点,连接 , .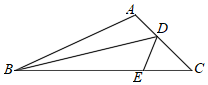 (1)、求证: ;(2)、若 ,求 的度数.23. 中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编(图1),书中记载了大量几何作图题,所有内容均用浅近的文言文表述,第一编记载了这样一道几何作图题:
(1)、求证: ;(2)、若 ,求 的度数.23. 中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编(图1),书中记载了大量几何作图题,所有内容均用浅近的文言文表述,第一编记载了这样一道几何作图题:原文
释义
甲乙丙为定直角.
以乙为圆心,以任何半径作丁戊弧;
以丁为圆心,以乙丁为半径画弧得交点己;
再以戊为圆心,仍以原半径画弧得交点庚;
乙与己及庚相连作线.
如图2, 为直角.
以点 为圆心,以任意长为半径画弧,交射线 , 分别于点 , ;
以点 为圆心,以 长为半径画弧与 交于点 ;
再以点 为圆心,仍以 长为半径画弧与 交于点 ;
作射线 , .
 (1)、根据以上信息,请你用不带刻度的直尺和圆规,在图2中完成这道作图题(保留作图痕迹,不写作法);(2)、根据(1)完成的图,直接写出 , , 的大小关系.24. 如图1,在等腰 中, ,点D为斜边AB边上一动点(不含端点).作 ,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
(1)、根据以上信息,请你用不带刻度的直尺和圆规,在图2中完成这道作图题(保留作图痕迹,不写作法);(2)、根据(1)完成的图,直接写出 , , 的大小关系.24. 如图1,在等腰 中, ,点D为斜边AB边上一动点(不含端点).作 ,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题: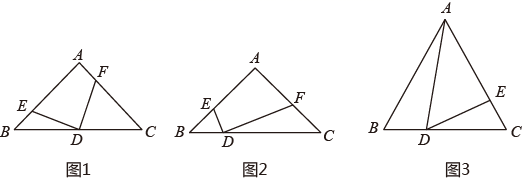 (1)、(问题发现)
(1)、(问题发现)
如图1,若点D为BC边中点.请直接写出DE,DF的数量关系.(2)、(类比探究)
如图2,若点D为BC边上一动点,且 .猜想DF与DE的数量关系.并证明你的结论.(3)、(拓展应用)
如图3,在边长为4的等边 中,点D为BC边上一动点,作 .DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.