2023年浙教版数学八年级下册第六章 反比例函数单元测试(进阶版)
试卷更新日期:2023-01-22 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 已知 是反比例函数,则函数的图象在( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限2. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( )
 A、1 B、 C、2 D、43. 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药时间小时之间函数关系如图所示(当时,与成反比例).血液中药物浓度不低于微克毫升的持续时间为( )
A、1 B、 C、2 D、43. 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药时间小时之间函数关系如图所示(当时,与成反比例).血液中药物浓度不低于微克毫升的持续时间为( ) A、 B、3 C、4 D、4. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示,当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A、 B、3 C、4 D、4. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示,当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( ) A、不大于m3 B、不小于m3 C、不大于m3 D、不小于m35. 如图,A、B是双曲线y=上的两点,经过A、B两点分别作AC∥y轴,BC∥x轴两线交于点C,已知S△AOC=3,S△ABC=9,则k的值为( )
A、不大于m3 B、不小于m3 C、不大于m3 D、不小于m35. 如图,A、B是双曲线y=上的两点,经过A、B两点分别作AC∥y轴,BC∥x轴两线交于点C,已知S△AOC=3,S△ABC=9,则k的值为( ) A、12 B、10 C、8 D、46. 两个反比例函数和在第一象限内的图象如图所示,点在的图象上,轴于点 , 交的图象于点 , 轴于点 , 交的图象于点 , 轴于点 , 当点在图象上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )
A、12 B、10 C、8 D、46. 两个反比例函数和在第一象限内的图象如图所示,点在的图象上,轴于点 , 交的图象于点 , 轴于点 , 交的图象于点 , 轴于点 , 当点在图象上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )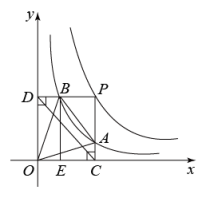 A、①②③ B、①②④ C、①③④ D、②③④7. 如图,直线AC与反比例函数y=(x>0)的图象交于A,C两点(点A在点C的左边),与x轴交于点B,以点A为顶点向下作矩形ADMN,其对角线相交于点O,且AD平分∠OAB,AC=CB,连结CD,若△ACD的面积为6,则k的值为( )
A、①②③ B、①②④ C、①③④ D、②③④7. 如图,直线AC与反比例函数y=(x>0)的图象交于A,C两点(点A在点C的左边),与x轴交于点B,以点A为顶点向下作矩形ADMN,其对角线相交于点O,且AD平分∠OAB,AC=CB,连结CD,若△ACD的面积为6,则k的值为( ) A、8 B、10 C、12 D、168. 如图,函数的图象经过斜边OB的中点C,连结AC.如果 , 那么的周长为( ).
A、8 B、10 C、12 D、168. 如图,函数的图象经过斜边OB的中点C,连结AC.如果 , 那么的周长为( ).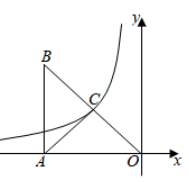 A、 B、 C、 D、9. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )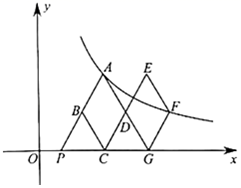 A、3 B、3 C、6 D、610. 如图,△OA1B1 , △A1A2B2 , △A2A3B3 , ……是分别以B1 , B2 , B3 , ……为直角顶点,斜边在x轴正半轴上的等腰直角三角形,其直角顶点B1(x1 , y1),B2(x2 , y2),B3(x3 , y3),……均在反比例函数y= (x>0)的图象上,则y1+y2+……+y10的值为( )
A、3 B、3 C、6 D、610. 如图,△OA1B1 , △A1A2B2 , △A2A3B3 , ……是分别以B1 , B2 , B3 , ……为直角顶点,斜边在x轴正半轴上的等腰直角三角形,其直角顶点B1(x1 , y1),B2(x2 , y2),B3(x3 , y3),……均在反比例函数y= (x>0)的图象上,则y1+y2+……+y10的值为( )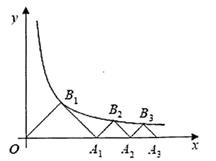 A、2 B、6 C、4 D、2
A、2 B、6 C、4 D、2二、填空题(每题3分,共18分)
-
11. 函数y= 是 反比例函数,则m的值是.12. 已知A(m,y1)、B(m+3,y2)是反比例函数y= 图象上两点,且y1﹣y2<0,则m的取值范围为 .13. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
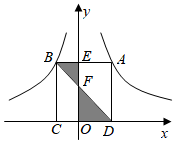 14. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为.
14. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为. 15. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=.
15. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=. 16. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .
16. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .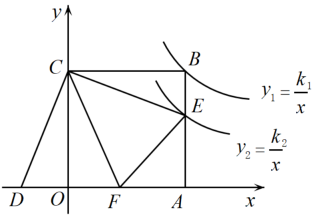
三、解答题(共8题,共72分)
-
17. 如图,在平面直角坐标系中,矩形ABCO的顶点A、C分别在x轴和y轴的正半轴上,顶点B的坐标为(4,2),双曲线(x>0)的图象交BC于点D,若BD= . 求反比例函数的解析式及点F的坐标.
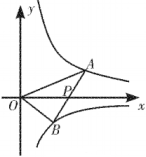
 18. 如图,点、分别在反比例函数和的图象上,线段与轴相交于点 .
18. 如图,点、分别在反比例函数和的图象上,线段与轴相交于点 .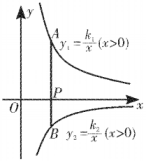
图① 图②
(1)、如图①,若轴,且 , . 求、的值;(2)、如图②,若点是线段的中点,且的面积为2.求的值.19. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.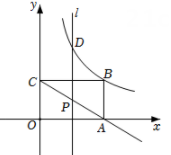 (1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.20. 如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y= (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y= 的另一个交点.
(1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.20. 如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y= (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y= 的另一个交点.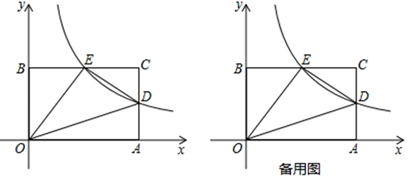 (1)、点D的坐标为 , 点E的坐标为;(2)、动点P在第一象限内,且满足
(1)、点D的坐标为 , 点E的坐标为;(2)、动点P在第一象限内,且满足①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
21. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 并与反比例函数的图象在第一象限相交于点 , 且点是的中点. (1)、如图1,求反比例函数的解析式;(2)、如图2,若矩形的顶点在直线上,顶点在点右侧的反比例函数图象上,顶点 , 在轴上,且 .
(1)、如图1,求反比例函数的解析式;(2)、如图2,若矩形的顶点在直线上,顶点在点右侧的反比例函数图象上,顶点 , 在轴上,且 .①求点的坐标;
②若点是反比例函数的图象第一象限上的动点,且在点的左侧,连结 , 并在左侧作正方形当顶点或顶点恰好落在直线上,直接写出对应的点的横坐标.
22. 已知点A(3,m+2),B(m+4,2)都在反比例函数y的图像上.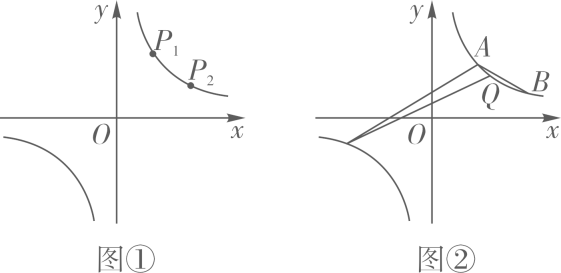 (1)、求m,k的值;(2)、如图①,已知反比例函数y的图像上有两点P1(x1 , y1),P2(x2 , y2),且0<x1<x2<3,分别过P1 , P2向x轴作垂线,垂足分别为M1 , M2 , 过P1 , P2向y轴作垂线,垂足分别为N1 , N2 . 若记四边形P1M1ON1和四边形P2M2ON2的周长分别为C1 , C2 , 试比较C1和C2的大小;并说明理由.(3)、如图②,若点B关于原点O对称点为C,点Q为双曲线AB段上任一动点,试探究∠ACQ与∠ABQ大小关系,并说明理由.23. 某市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为 的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚里温度 随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线 的一部分,请根据图中信息解答下列问题.
(1)、求m,k的值;(2)、如图①,已知反比例函数y的图像上有两点P1(x1 , y1),P2(x2 , y2),且0<x1<x2<3,分别过P1 , P2向x轴作垂线,垂足分别为M1 , M2 , 过P1 , P2向y轴作垂线,垂足分别为N1 , N2 . 若记四边形P1M1ON1和四边形P2M2ON2的周长分别为C1 , C2 , 试比较C1和C2的大小;并说明理由.(3)、如图②,若点B关于原点O对称点为C,点Q为双曲线AB段上任一动点,试探究∠ACQ与∠ABQ大小关系,并说明理由.23. 某市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为 的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚里温度 随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线 的一部分,请根据图中信息解答下列问题. (1)、恒温系统在这天保持大棚内温度为 的时间有多少小时?(2)、求 的值.(3)、恒温系统在一天24h内保持大棚温度在 的时间有多少小时?24. 某一农家计划利用已有的一堵长为8m的墙,用篱笆圈成一个面积为12m2的矩形ABCD花园,现在可用的篱笆总长为11m.
(1)、恒温系统在这天保持大棚内温度为 的时间有多少小时?(2)、求 的值.(3)、恒温系统在一天24h内保持大棚温度在 的时间有多少小时?24. 某一农家计划利用已有的一堵长为8m的墙,用篱笆圈成一个面积为12m2的矩形ABCD花园,现在可用的篱笆总长为11m.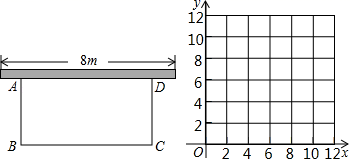 (1)、若设 , .请写出y关于x的函数表达式;(2)、若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;(3)、若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.
(1)、若设 , .请写出y关于x的函数表达式;(2)、若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;(3)、若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.