2023年浙教版数学八年级下册6.3反比例函数的应用同步测试

试卷更新日期：2023-01-22 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，一次函数 $y = k x + b (k$ 、 $b$ 为常数， $k \neq 0)$ 与反比例函数 $y = \frac{4}{x}$ 的图象交于A（1，m），B（n，2）两点，与坐标轴分别交于 $M$ ， $N$ 两点．则△AOB的面积为（）

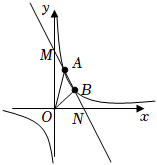A、3 B、6 C、8 D、12

查看试题解析
2. 要确定方程 $x^{2} + x - 5 = 0$ 的解，只需知道一次函数 $y = x + 1$ 和反比例函数 $y = \frac{k}{x}$ 的图象交点的横坐标．由上面的信息可知， $k$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
3. 已知正比例函数y=k₁x（k₁≠0）的图象与反比例函数y= $\frac{k_{2}}{x}$ （k₂≠0）的图象交于点A（-1，2），B（m，n），则点B的坐标是（）

A、（2，-1） B、（1，-2） C、（1，2） D、（-1，-2）

查看试题解析
4. 如果矩形的面积为6cm² ，那么它的长ycm与宽xcm之间的函数关系用图象表示大致是（）

A、 B、 C、 D、

查看试题解析
5. 如图是一个闭合电路，其电源的电压为定值，电流I（A）是电阻R（ $Ω$ ）的反比例函数．当 $R = 2 Ω$ 时， $I = 6 A$ ．若电阻R增大 $1 Ω$ ，则电源I为（）

A、3A B、4A C、7A D、12A

查看试题解析
6. 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是1200N和0.5m，则动力F(单位：N)关于动力臂l(单位：m)的函数表达式正确的是（）

A、 $F = \frac{1200}{l}$ B、 $F = \frac{600}{l}$ C、 $F = \frac{500}{l}$ D、 $F = \frac{0.5}{l}$

查看试题解析
7. 某电子商城推出分期付款购买电脑的活动，一台电脑的售价为1.2万元，前期付款4000元，后期每个月分期付一定的数额，则每个月的付款额 $y$ (元)与付款月数 $x$ 之间的函数关系式是（）

A、 $y = \frac{8000}{x}$ （x为正整数) B、 $y = \frac{8}{x}$ C、 $y = \frac{8000}{x}$ D、 $y = 8000 x$

查看试题解析
8. 某气球内充满一定质量的气体，温度不变时，气球内气体的压强 $p (kPa)$ 与气体的体积 $V (m^{3})$ 的关系是如图所示的反比例函数．当气球内气体的压强大于200kPa，气球就会爆炸．为了不让气球爆炸，则气球内气体的体积 $V$ 需满足的取值范围是（）

A、 $V < 0.5$ B、 $V > 0.5$ C、 $V \leq 0.5$ D、 $V \geq 0.5$

查看试题解析
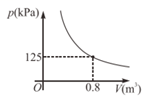9. 某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V(m³)的反比例函数，且当V=1.5m³时，p=16000Pa，当气球内的气压大于40000Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应(　　)

A、不小于0.5m³ B、不大于0.5m³ C、不小于0.6m³ D、不大于0.6m³

查看试题解析
10. 某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P(kPa)是气球体积V(m³)的反比例函数，其图象如图所示，当气球内的气压大于120 kPa时，气球将爆炸，为了安全，气球的体积应该（）

A、不夫于 $\frac{5}{4} m^{3}$ B、小于 $\frac{5}{4} m^{3}$ C、不小于 $\frac{4}{5} m^{3}$ D、小于 $\frac{4}{5} m^{3}$

查看试题解析

二、填空题（每题4分，共24分）

11. 已知一次函数 $y_{1} = a x + b$ 与反比例函数 $y_{2} = \frac{k}{x}$ 的图象如图所示．在第一象限内，当 $y_{1} > y_{2}$ 时，则 $x$ 的取值范围是．

查看试题解析
12. 密闭容器内有一定质量的二氧化碳，在温度不变的情况下，当容器的体积V（单位：m³）变化时，气体的密度ρ（单位：kg/m³）随之变化，已知密度ρ是体积V的反比例函数关系，它的图象如图所示，则当ρ = 3.3 kg/m³时，相应的体积V是 m³.

查看试题解析
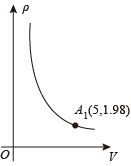13. 小明要把一篇文章录入电脑，所需时间 $y (\min)$ 与录入文字的速度 $x$ （字 $/ \min$ ）之间的反比例函数关系如图所示，如果小明要在 $9 \min$ 内完成录入任务，则小明录入文字的速度至少为字 $/ \min$ .

查看试题解析

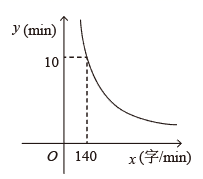14. 已知一次函数y＝

\frac{1}{2}

x＋b与反比例函数y＝

\frac{4}{x}

中，x与y的对应值如下表：

x	……	-4	-3	-2	-1	1	2	3	……
y= $\frac{1}{2}$ ＋b	……	-1	- $\frac{1}{2}$	0	$\frac{1}{2}$	$\frac{3}{2}$	2	$\frac{5}{2}$	……
y= $\frac{4}{x}$	……	-1	- $\frac{4}{3}$	-2	-4	4	2	$\frac{4}{3}$	……

则不等式 $\frac{1}{2}$ x＋b ＜ $\frac{4}{x}$ 的解集为.

查看试题解析

15. 王华和王强同学在合作电学实验时，记录下电流

I

(A)与电阻

R (Ω)

有如下对应关系.观察下表.

R	…	2	4	8	10	16	…
$I$	…	16	8	4	3.2	2	…

你认为 $I$ 与 $R$ 间的函数关系式为；当电阻 $R = 5 Ω$ 时，电流 $I =$ A.

查看试题解析

16. 已知近视眼镜的度数D（度）与镜片焦距f（米）成反比例关系，且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜，经过一段时间的矫正治疗后，现在只需戴镜片焦距为0.4米的眼镜了，则小慧所戴眼镜的度数降低了度.

查看试题解析

三、解答题（共8题，共66分）

17. 已知一次函数 $y = 3 x - m$ 和反比例函数 $y =$ $\frac{m - 3}{x}$ .当 $y = 2$ 时，两个函数自变量的值相等，求反比例函数的表达式.

查看试题解析
18. 甲工程队新建公路，每名工人每天工作8小时，则甲工程队每天可完成600米新建公路．乙工程队比甲工程队少10名工人，每名工人每天工作10小时，则乙工程队每天可完成500米新建公路，假定甲、乙两工程队的每名工人每小时完成的工作量相同，求乙工程队的工人有多少名？

查看试题解析
19. 某蔬菜生产基地在气温较低时用装有恒温系统的大棚栽培一种在自然光照且温度为 $18 ℃$ 的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后大棚内的温度 $y (℃)$ 随时间 $x$ （小时）变化的函数图象，其中 $B C$ 段是双曲线 $y = \frac{k}{x}$ 的一部分.请根据图中信息解答下列问题：

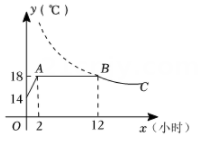(1)、恒温系统在这天保持大棚内的温度 $18 ℃$ 的时间有小时；

(2)、 $k =$ ；

(3)、当棚内温度不低于 $16 ℃$ 时，该蔬菜能够快速生长，则这天该蔬菜能够快速生长小时.

查看试题解析
20. 为了做好校园疫情防控工作，学校后勤每天对全校办公室和教室进行药物喷洒消毒，完成1间教室的药物喷洒要5min ，药物喷洒时教室内空气中的药物浓度 $y$ （单位： ${mg/m}^{3}$ ）与时间 $x$ （单位：min）的函数关系式为 $y = 2 x$ ，其图象为图中线段 $O A$ ，药物喷洒完成后 $y$ 与 $x$ 成反比例函数关系，两个函数图象的交点为 $A (m ， n)$ ，当教室空气中的药物浓度不高于 ${1mg/m}^{3}$ 时，对人体健康无危害，如果后勤人员依次对一班至十一班教室（共11间）进行药物喷洒消毒当最后一间教室药物喷洒完成后，一班能否能让人进入教室？请通过计算说明.

查看试题解析
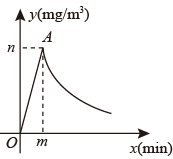21. 某科技小组野外考察时遇到一片烛泥湿地，为了安全、迅速通过这片湿地，他们沿着前进的路线铺了若干块木板，构成了一条临时通道.若人和木板对湿地地面的压力 $F$ 一定时，木板对烪泥湿地的压强 $p (Pa)$ 是木板面积 $S (m^{2})$ 的反比例函数，其图象如图所示.

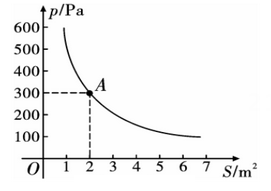(1)、求出 $p$ 与 $S$ 的函数表达式；

(2)、当木板面积为 $0.3 m^{2}$ 时，压强是多少?

查看试题解析
22. 如图，在平面直角坐标系中，直线 $y_{1} = k_{1} x + b$ 与双曲线 $y_{2} = \frac{k_{2}}{x}$ 相交于 $A (4 ， 2)$ 、 $B (m ， - 4)$ 两点．

(1)、求 $y_{1} ， y_{2}$ 对应的函数表达式．

(2)、过点B作 $B P ⊥ x$ 轴于点P，求 $△ A B P$ 的面积．

(3)、根据函数图象，直接写出关于x的不等式 $k_{1} x + b > \frac{k_{2}}{x}$ 的解集．

查看试题解析
23. 王老师驾驶小汽车从A地行驶到B地，行驶里程为480千米，设小汽车的行驶时间为t（单位：小时），行驶的平均速度为v（单位：千米/小时），且全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、王老师上午8点驾驶小汽车从A地出发.
①王老师需要在当天13点至14点（含13点和14点）间到达B地，求小汽车行驶的平均速度v需达到的范围；
②王老师能否在当天11点30分前到达B地？说明理由.

查看试题解析
24. 定义：只有三边相等的四边形称为准菱形.

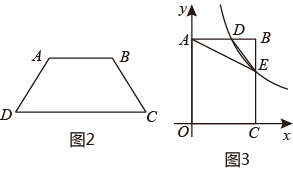(1)、如图1，图形（填序号）是准菱形；

(2)、如图2，四边形ABCD中，AB∥DC，∠B+∠D＝180°，AB＝AD，求证：四边形ABCD是准菱形；

(3)、如图3，在平面直角坐标系xOy中，矩形OABC的边OA，OC分别落在y轴，x轴上，反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象分别与边AB，BC交于点D，E.已知AD＝DE，△ADE的面积为10，AD：DB＝5：3，若点F是坐标平面上一点，四边形ADEF是准菱形，当准菱形ADEF面积最大时，求点F的坐标.

查看试题解析

2023年浙教版数学八年级下册6.3反比例函数的应用 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学八年级下册6.3反比例函数的应用同步测试