2023年浙教版数学八年级下册6.2反比例函数的图象与性质同步测试

试卷更新日期：2023-01-22 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点（3，-5），则该反比例函数的图象位于（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限

查看试题解析
2. 关于反比例函数 $y = \frac{3}{x}$ ，下列说法错误的是（）

A、图象关于原点对称 B、y随x的增大而减小 C、图象分别位于第一、三象限 D、若点 $M (a ， b)$ 在其图象上，则 $a b = 3$

查看试题解析
3. 已知正比例函数 $y = \frac{x}{k}$ 中，y的值随x的值的增大而增大，那么它和反比例函数 $y = \frac{k}{x}$ 在同一平面直角坐标系内的大致图像可能是（）

A、 B、 C、 D、

查看试题解析
4. 若抛物线y=ax²经过点P（- $\sqrt{7}$ ， 4），则该抛物线一定还经过点（）

A、（4，- $\sqrt{7}$ ） B、（- $\sqrt{7}$ ， -4） C、（-4， $\sqrt{7}$ ） D、（ $\sqrt{7}$ ， 4）

查看试题解析
5. 若点 $A (x_{1} ， - 5)$ ， $B (x_{2} ， 2)$ ， $C (x_{3} ， 5)$ 都在反比例函数 $y = \frac{10}{x}$ 的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} < x_{1} < x_{3}$ C、 $x_{1} < x_{3} < x_{2}$ D、 $x_{3} < x_{1} < x_{2}$

查看试题解析
6. 已知函数y₁ $= \frac{k}{x}$ （k为常数，且k＞0，x＞0），函数y₂的图象和函数y₁的图象关于直线y＝1对称．
①函数y₂的图象上的点的纵坐标都小于2．②若当m≤x≤2（m为大于0的实数）时，y₁的最大值为a，则在此取值范围内，y₂的最小值必为2﹣a．则下列判断正确的是（）

A、①②都正确 B、①正确，②错误 C、①错误，②正确 D、①②都错误

查看试题解析
7. 如图，点B在y轴的正半轴上，点C在反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上，菱形 $O A B C$ 的面积为8，则k的值为（）

A、-4 B、4 C、-2 D、2

查看试题解析
8. 如图，已知双曲线 $y = \frac{k}{x} (k < 0)$ 经过 $R t △ O A B$ 斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为 $(- 6 ， 4)$ ，则 $△ A O C$ 的面积为（）

A、 $\frac{9}{2}$ B、6 C、9 D、10

查看试题解析
9. 已知点A（3，4）在反比例函数 $y = \frac{k}{x} (k$ 为常数， $k \neq 0)$ 的图象上，则该反比例函数的解析式是（）

A、 $y = \frac{3}{x}$ B、y= $\frac{4}{x}$ C、y= $\frac{12}{x}$ D、y= $\frac{7}{x}$

查看试题解析
10. 如图，平行四边形 $A B C O$ 的顶点 $B$ 在双曲线 $y = \frac{6}{x}$ 上，顶点 $C$ 在双曲线 $y = \frac{k}{x}$ 上， $B C$ 中点 $P$ 恰好落在 $y$ 轴上，已知 $S_{▱ O A B C} = 10$ ，则 $k$ 的值为（）

A、-8 B、-6 C、-4 D、-2

查看试题解析

二、填空题（每题4分，共24分）

11. 某工程队计划修建铁路，给出了铺轨的天数y（d）与每日铺轨量x（km/d）之间的关系表：
y（d）
120
150
200
240
300
x（km/d）
10
8
6
5
4
根据表格信息，判断出y是x的函数，则这个函数表达式是．

查看试题解析
12. 已知反比例函数 $y = \frac{k}{x}$ 的图象分别位于第一、第三象限，则实数k的值可以是．（只需写出一个符合条件的实数）

查看试题解析
13. 正比例函数 $y = k x$ 与反比例函数 $y = \frac{1}{x}$ 的图象交于 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 两点，则代数式 $x_{1} y_{2} + x_{2} y_{1}$ 的值是.

查看试题解析
14. 如果点 $(2 ， a)$ 、 $(3 ， b)$ 在反比例函数 $y = \frac{k}{x}$ $(k \neq 1)$ 的图象上，若 $a < b$ ，则k0（用“<”或“>”号连接）

查看试题解析
15. 如图，点A是反比例函数 $y = \frac{k}{x} (x < 0)$ 图象上一点，过点A作 $A B ⊥ y$ 轴于点D，且点D为线段AB的中点，若点C为x轴上任意一点，且 $△ A B C$ 的面积为4，则k的值为．

查看试题解析
16. 如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE．若AD平分∠OAE，反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图象经过AE上的两点A，F，且AF＝EF，△ABE的面积为18，则k的值为．

查看试题解析

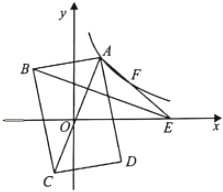
三、解答题（共8题，共66分）

17. 已知反比例函数y= $\frac{n + 6}{x}$ 的图象经过第二、四象限，求n的取值范围．

查看试题解析
18. 如图，点A，B关于y轴对称，S_△AOB＝8，点A在双曲线y＝ $\frac{2 k}{x}$ ，求k的值.

查看试题解析
19. 在平面直角坐标系内，点 $O$ 为坐标原点，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $A$ ， $B$ 两点，若 $A (4, 1)$ ，点 $B$ 的横坐标为 $- 2$ ，求反比例函数及一次函数的解析式．

查看试题解析
20. 如图，在平面直角坐标系中．四边形 $O A B C$ 为矩形，点 $C$ 、 $A$ 分别在 $x$ 轴和 $y$ 轴的正半轴上，点 $D$ 为 $A B$ 的中点已知实数 $k \neq 0$ ，一次函数 $y = - 3 x + k$ 的图像经过点 $C$ 、 $D$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像经过点 $B$ ，求 $k$ 的值．

查看试题解析
21. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(2 ， 2)$ ．

(1)、求这个反比例函数的表达式；

(2)、当 $- 3 < x < - 1$ 时，求 $y$ 的取值范围．

查看试题解析
22. 综合与探究
如图1，反比例函数的图象 $y = - \frac{8}{x}$ 经过点A，点A的横坐标是－2，点A关于坐标原点O的对称点为点B，作直线 $A B$ ．

(1)、判断点B是否在反比例函数 $y = - \frac{8}{x}$ 的图象上，并说明理由；

(2)、如图1，过坐标原点O作直线交反比例函数 $y = - \frac{8}{x}$ 的图象于点C和点D，点C的横坐标是4，顺次连接 $A D$ ， $D B$ ， $B C$ 和 $C A$ ．求证：四边形 $A C B D$ 是矩形；

(3)、已知点P在x轴的正半轴上运动，点Q在平面内运动，当以点O，B，P和Q为顶点的四边形为菱形时，请直接写出此时点P的坐标．

查看试题解析
23. 背景：点A在反比例函数y $= \frac{k}{x}$ （k＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形．如图1，点A在第一象限内，当AC＝4时，小李测得CD＝3．
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系．请帮助小李解决下列问题．

(1)、求k的值．

(2)、设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”．如图2，小李画出了x＞0时“Z函数”的图象．
①求这个“Z函数”的表达式；

②补画x＜0时“Z函数”的图象；

③并写出这个函数的性质（两条即可）．

查看试题解析
24. 已知一块矩形草坪的两边长分别是2米与3米，现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍，设原矩形的一边加长 $a$ 米，另一边长加长 $b$ 米，可得 $a$ 与 $b$ 之间的函数关系式 $b = \frac{12}{a + 3} - 2.$ 某班“数学兴趣小组”对此函数进一步推广，得到更一般的函数 $y = \frac{12}{x + 3} - 2$ ，现对这个函数的图象和性质进行了探究，研究过程如下，请补充完整：

(1)、类比反比例函数可知，函数 $y = \frac{12}{x + 3} - 2$ 的自变量 $x$ 的取值范围是，这个函数值 $y$ 的取值范围是．

(2)、“数学兴趣小组”进一步思考函数 $y = | \frac{12}{x + 3} - 2 |$ 的图象和性质，请根据函数 $y = \frac{12}{x + 3} - 2$ 的图象，画出函数 $y = | \frac{12}{x + 3} - 2 |$ 的图象；

(3)、结合函数 $y = | \frac{12}{x + 3} - 2 |$ 的图象解答下列问题：
①求出方程 $| \frac{12}{x + 3} - 2 | = 0$ 的根；

②如果方程 $| \frac{12}{x + 3} - 2 | = a$ 有2个实数根，请直接写出 $a$ 的取值范围．

查看试题解析

y（d）	120	150	200	240	300
x（km/d）	10	8	6	5	4

2023年浙教版数学八年级下册6.2反比例函数的图象与性质 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学八年级下册6.2反比例函数的图象与性质同步测试