2023年浙教版数学八年级下册第五章 特殊平行四边形 单元测试 (基础版)
试卷更新日期:2023-01-22 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,矩形ABCD中, , 点E在边AD上,EB平分∠AEC,∠DEC=30°,则AE长为( )
 A、1 B、 C、 D、2. 如图,点O是矩形的对角线的中点,点M是的中点.若 , 则四边形的周长是( )
A、1 B、 C、 D、2. 如图,点O是矩形的对角线的中点,点M是的中点.若 , 则四边形的周长是( )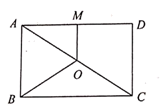 A、7 B、8 C、9 D、103. 如图,矩形的对角线、相交于点 , , , , 若 , 则四边形的周长为( )
A、7 B、8 C、9 D、103. 如图,矩形的对角线、相交于点 , , , , 若 , 则四边形的周长为( ) A、4 B、8 C、10 D、124. 如图,周长为24的菱形中, , 点E,F分别是边上的动点,点P为对角线上一动点,则线段的最小值为( )
A、4 B、8 C、10 D、124. 如图,周长为24的菱形中, , 点E,F分别是边上的动点,点P为对角线上一动点,则线段的最小值为( ) A、 B、 C、 D、5. 菱形中,对角线与的长分别为6和8,则该菱形的周长为( )A、 B、20 C、 D、406. 下列命题中,错误的是( )A、两组对边分别相等的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、有一组邻边相等的矩形是正方形7. 如图,四边形是平行四边形,下列结论中错误的是( )
A、 B、 C、 D、5. 菱形中,对角线与的长分别为6和8,则该菱形的周长为( )A、 B、20 C、 D、406. 下列命题中,错误的是( )A、两组对边分别相等的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、有一组邻边相等的矩形是正方形7. 如图,四边形是平行四边形,下列结论中错误的是( ) A、当时,是菱形 B、当时,是矩形 C、当时,是菱形 D、当且时,是正方形8. 已知四边形是矩形,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A、当时,是菱形 B、当时,是矩形 C、当时,是菱形 D、当且时,是正方形8. 已知四边形是矩形,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( ) A、 B、 C、 D、9. 下列说法正确的是( )A、三条边相等的四边形是菱形 B、对角线相等的平行四边形是矩形 C、连接矩形各边中点所得四边形是正方形 D、一组对边平行,另一组对边相等的四边形是平行四边形10. 新冠疫情防控过程中,某中学在大门口的正上方A处装着一个红外线激光测温仪,离地米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生(米)正对门缓慢走到离门1.2米的地方时(米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A、 B、 C、 D、9. 下列说法正确的是( )A、三条边相等的四边形是菱形 B、对角线相等的平行四边形是矩形 C、连接矩形各边中点所得四边形是正方形 D、一组对边平行,另一组对边相等的四边形是平行四边形10. 新冠疫情防控过程中,某中学在大门口的正上方A处装着一个红外线激光测温仪,离地米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生(米)正对门缓慢走到离门1.2米的地方时(米),测温仪自动显示体温,则人头顶离测温仪的距离等于( ) A、1.2米 B、1.3米 C、1.4米 D、1.5米
A、1.2米 B、1.3米 C、1.4米 D、1.5米二、填空题(每题4分,共28分)
-
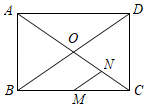
11. 如图,在矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点,若MN=4,则AC的长为 ;若△BOC的面积为5,则矩形ABCD的面积为 .
 12. 在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是 .13. 木工师傅要做一张长方形的桌面.完成后,量得桌面的长为 , 宽为 , 对角线为130cm,则做出的这个桌面.(填“合格”或“不合格”)14. 菱形的两条对角线长分别是6和8,则此菱形的面积是 .15. 两个全等菱形如图所示摆放在一起,其中 和 分别在同一条直线上,若较短的对角线长为10,点 与点 的距离是24,则此菱形边长为.
12. 在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是 .13. 木工师傅要做一张长方形的桌面.完成后,量得桌面的长为 , 宽为 , 对角线为130cm,则做出的这个桌面.(填“合格”或“不合格”)14. 菱形的两条对角线长分别是6和8,则此菱形的面积是 .15. 两个全等菱形如图所示摆放在一起,其中 和 分别在同一条直线上,若较短的对角线长为10,点 与点 的距离是24,则此菱形边长为. 16. 如图,在正方形ABCD中,E是AD上一点、连接CE,交BD于点F,若AD=BF,则∠DEF=°.
16. 如图,在正方形ABCD中,E是AD上一点、连接CE,交BD于点F,若AD=BF,则∠DEF=°. 17. 如图,在△ABC中,点D,E,F分别是△ABC的边AB,BC,AC上的点,且DE∥AC,EF∥AB,要使四边形ADEF是正方形,还需添加条件:.
17. 如图,在△ABC中,点D,E,F分别是△ABC的边AB,BC,AC上的点,且DE∥AC,EF∥AB,要使四边形ADEF是正方形,还需添加条件:.
三、作图题(共9分)
-
18. 图1,图2,图3,图4是四张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,A,C两点都在格点上,连结AC,请完成下列作图:
 (1)、以AC为对角线在图1中作一个正方形,且正方形各顶点均在格点上.(2)、以AC为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.(3)、以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形(不含矩形),且平行四边形顶点在格点上.
(1)、以AC为对角线在图1中作一个正方形,且正方形各顶点均在格点上.(2)、以AC为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.(3)、以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形(不含矩形),且平行四边形顶点在格点上.四、解答题(共6题,共47分)
-
19. 如图,在中, , , , , 是的中位线.求证:四边形是矩形.
 20. 如图所示,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.
20. 如图所示,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.求证:四边形BEDF是正方形.
 21. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.
21. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.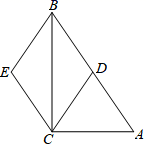 22. 如图,在四边形中,点 , , , 分别为边 , , , 的中点.
22. 如图,在四边形中,点 , , , 分别为边 , , , 的中点. (1)、求证:四边形是平行四边形.(2)、若四边形的对角线互相垂直且它们的乘积为48,求四边形的面积.23. 如图,▱ABCD的对角线AC,BD相交于点O,过点O作EF⊥AC,分别交AB,DC于点E,F,连接AF,CE.
(1)、求证:四边形是平行四边形.(2)、若四边形的对角线互相垂直且它们的乘积为48,求四边形的面积.23. 如图,▱ABCD的对角线AC,BD相交于点O,过点O作EF⊥AC,分别交AB,DC于点E,F,连接AF,CE. (1)、若OE= ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.24. 如图
(1)、若OE= ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.24. 如图


如图1,在正方形ABCD中,点P是对角线BD上的一点,连结CP.
(1)、求证:△ADP≌△CDP;(2)、如图2,延长AP交线段DC于点Q , 交BC的延长线于点G , 点M是GQ的中点,连结CM . 求证:PC⊥MC;(3)、如图3,延长AP交射线DC于点Q , 交BC于点G , 点M是GQ的中点,连结CM . 若PM=2, ∠BAP=30°.求AB的长.
-