2023年浙教版数学八年级下册5.3正方形 同步测试
试卷更新日期:2023-01-22 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 正方形具有而菱形不一定具有的特征是( )A、对边互相平行 B、对角线互相垂直平分 C、中心对称图形 D、有4条对称轴2. 如图,延长正方形边至点E,使 , 则为( )
 A、22.5° B、25° C、30° D、45°3. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( )
A、22.5° B、25° C、30° D、45°3. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( ) A、2 B、4 C、8 D、4. 如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为 , , 有如下三个结论:
A、2 B、4 C、8 D、4. 如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为 , , 有如下三个结论:①正方形ABCD的面积等于的一半;②正方形EFGH的面积等于的一半;③ .

上述结论中,所有正确结论的序号是( )
A、①② B、②③ C、③ D、①②③5. 根据特殊四边形的定义,在图中的括号内①、②、③、④处应填写的内容是( ) A、平行四边形;一个角为60°;矩形;一组邻边相等 B、平行四边形;一组邻边相等;矩形;一组邻边相等 C、矩形;一个角为60°;平行四边形;一组邻边相等 D、矩形;一组邻边相等;平行四边形;一组邻边相等6. 在四边形ABCD中, . 如果再添加一个条件可证明四边形是正方形,那么这个条件可以是( )A、 B、 C、 D、7. 如图在边长为1的小正方形构成的5×4的网格中,定义:以网格中的格点为顶点的正方形叫做格点正方形.则图中完全包含“
A、平行四边形;一个角为60°;矩形;一组邻边相等 B、平行四边形;一组邻边相等;矩形;一组邻边相等 C、矩形;一个角为60°;平行四边形;一组邻边相等 D、矩形;一组邻边相等;平行四边形;一组邻边相等6. 在四边形ABCD中, . 如果再添加一个条件可证明四边形是正方形,那么这个条件可以是( )A、 B、 C、 D、7. 如图在边长为1的小正方形构成的5×4的网格中,定义:以网格中的格点为顶点的正方形叫做格点正方形.则图中完全包含“ ”的格点正方形最多能画( )
”的格点正方形最多能画( )
 A、13个 B、16个 C、19个 D、21个8. 如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
A、13个 B、16个 C、19个 D、21个8. 如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( ) A、2 B、 C、 D、9. 将图1中两个三角形按图2所示的方式摆放,其中四边形为矩形,连接 , , 甲、乙两人有如下结论:
A、2 B、 C、 D、9. 将图1中两个三角形按图2所示的方式摆放,其中四边形为矩形,连接 , , 甲、乙两人有如下结论:甲:若四边形为正方形,则四边形必是正方形;
乙:若四边形为正方形,则四边形必是正方形.
下列判断正确的是( )
 A、甲正确,乙错误 B、甲错误,乙正确 C、甲、乙都错误 D、甲、乙都正确10. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A、甲正确,乙错误 B、甲错误,乙正确 C、甲、乙都错误 D、甲、乙都正确10. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( ) A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题(每题4分,共24分)
-
11. 已知正方形ABCD的边长为6,如果P是正方形内一点,且 , 那么AP的长为 .12. 在四边形ABCD中,对角线AC,BD交于点O,OA=OC=OB=OD,添加一个条件使四边形ABCD是正方形,那么所添加的条件可以是(写出一个即可)13. 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是 .
 14. 如图,正方形ABCD的边长为4,点M在AB上,且 , N是BD上一动点,则的最小值为 .
14. 如图,正方形ABCD的边长为4,点M在AB上,且 , N是BD上一动点,则的最小值为 . 15. 如图,点 , , , 为正方形 四边中点,连结 , , , 若 ,则四边形 的面积是.
15. 如图,点 , , , 为正方形 四边中点,连结 , , , 若 ,则四边形 的面积是.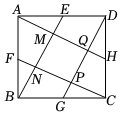 16. 在中 , 点O是对角线的中点.过点O作直线 , 直线分别交于点H,F,直线分别交于点G,E.连接.有下列四个结论:
16. 在中 , 点O是对角线的中点.过点O作直线 , 直线分别交于点H,F,直线分别交于点G,E.连接.有下列四个结论:①四边形可以是平行四边形;②四边形可以是矩形;③四边形不可以是菱形;④四边形不可以是正方形,其中正确的是.(写出所有正确结论的序号)
三、作图题(共9分)
-
17. 如图,在4×4的网格中每个小正方形边长都是1,每个小格的顶点叫做格点,线段AB的两个端点都在格点上,以格点为顶点分别按下列要求画图.

( 1 )在图①中,以AB为一边画平行四边形ABCD , 使其面积为6;
( 2 )在图②中,以AB为一边画菱形ABEF;
( 3 )在图③中,以AB为一边画正方形ABGH , 且与图②中所画的图形不全等.
四、解答题(共7题,共60分)
-
18. 小明同学从一张面积为5的正方形Ⅰ中剪出一个面积为2的小正方形Ⅱ,并按如图所示摆放,其中A,B,C三点共线,求线段AD的长.
 19. 如图,四边形ABCD是一个正方形花园,E、F是它的两个门,且 , 要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?请证明你的猜想.
19. 如图,四边形ABCD是一个正方形花园,E、F是它的两个门,且 , 要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?请证明你的猜想. 20. 已知:如图,在Rt中,平分交于点 , 垂足分别为 , 求证:四边形是正方形.
20. 已知:如图,在Rt中,平分交于点 , 垂足分别为 , 求证:四边形是正方形. 21. 如图,已知四边形和均是正方形,点K在上,延长到点H,使 , 连接 .
21. 如图,已知四边形和均是正方形,点K在上,延长到点H,使 , 连接 . (1)、求证:;(2)、求证:四边形是正方形;(3)、若四边形的面积为10, , 求点之间的距离.22. 如图,△ABC中,交AC于P,∠ACB,∠ACD的平分线分别交MN于E、F.
(1)、求证:;(2)、求证:四边形是正方形;(3)、若四边形的面积为10, , 求点之间的距离.22. 如图,△ABC中,交AC于P,∠ACB,∠ACD的平分线分别交MN于E、F. (1)、求证:;(2)、当MN与AC的交点P在AC的什么位置时,四边形AECF是矩形,说明理由;(3)、当△ABC满足什么条件时,四边形AECF是正方形.(不需要证明)23. 如图, , 为平行四边形 的对角线,点E是 上一点,点F在 延长线
(1)、求证:;(2)、当MN与AC的交点P在AC的什么位置时,四边形AECF是矩形,说明理由;(3)、当△ABC满足什么条件时,四边形AECF是正方形.(不需要证明)23. 如图, , 为平行四边形 的对角线,点E是 上一点,点F在 延长线上,且 , 与 交于点G,连结 .
 (1)、求证: .(2)、连结 , ,若 ,且G恰好是 的中点,求证:四边形 是菱形.(3)、在(2)的条件下,若四边形 是正方形,且 ,求 的长.24. 知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
(1)、求证: .(2)、连结 , ,若 ,且G恰好是 的中点,求证:四边形 是菱形.(3)、在(2)的条件下,若四边形 是正方形,且 ,求 的长.24. 知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.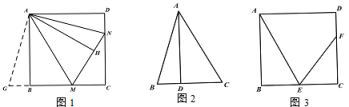 (1)、知识探究:在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;(2)、知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为;(3)、知识拓展:如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.
(1)、知识探究:在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;(2)、知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为;(3)、知识拓展:如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.
-