2023年浙教版数学八年级下册5.2菱形 同步测试

试卷更新日期：2023-01-22 类型：同步测试

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 如图，菱形ABCD的对角线AC、BD相交于点O，BD＝6，AC＝8，E是CD的中点，则OE的长是（  ）

    A、2.5 B、3 C、4 D、5

    查看试题解析

  • 2. 已知AB=AD ， 用没有刻度的直尺和圆规作菱形ABCD ， 下面的作法中正确的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 张师傅应客户要求加工4个菱形零件．在交付客户之前，需要对4个零件进行检测．根据零件的检测结果，图中有可能不合格的零件是（  ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（  ）

    A、40cm B、30cm C、20cm D、10cm

    查看试题解析

  • 5. 如图，菱形ABCD中，∠ABC=150° ， DH⊥AB于H ， 交对角线AC于E ， 过E作EF⊥AD于F ． 若△DEF的周长为3+3 ， 则菱形ABCD的面积为（ ）

    A、18 B、14+83 C、7+43 D、12+63

    查看试题解析

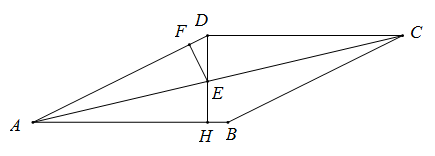  • 6. 如图，在四边形ABCD中，对角线AC、BD相交于点O，OA=OC，请你添加一个条件，使四边形ABCD是平行四边形，你添加的条件是（  ）

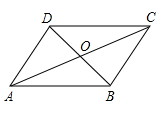    A、AC=BD B、OA=OB C、OA=AD D、OB=0D

    查看试题解析

  • 7. 如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处，易证四边形AECF是平行四边形．当∠BAE为（       ）度时，四边形AECF是菱形．

    A、30° B、40° C、45° D、50°

    查看试题解析

  • 8. 在一组对边平行的四边形中，增加一个条件，使得这个四边形是菱形，那么增加的条件可以是（       ）
    A、另一组对边相等，对角线相等 B、另一组对边相等，对角线互相垂直 C、另一组对边平行，对角线相等 D、另一组对边平行，对角线相互垂直

    查看试题解析

  • 9. 如图，菱形ABCD的边长为6，∠D=120° ， 点E是AB的中点，点P是对角线AC上一动点，则BP+EP的最小值是（ ）

    A、33 B、63 C、3 D、62

    查看试题解析

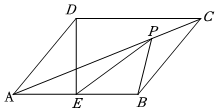  • 10. 如图1，在菱形ABCD中，对角线AC、BD相交于O，要在对角线BD上找两点M、N，使得四边形AMCN是菱形，现有图2中的甲、乙两种方案，则正确的方案是（  ）

    A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是

    查看试题解析

二、填空题（每题4分，共24分）

  • 11. 如图，在平面直角坐标系中，菱形OABC的顶点B的坐标为(8，4)，则C点的坐标为 ．

    查看试题解析

  • 12. 已知平行四边形的一边长为3，两条对角线的长分别为4和25 ， 则这个平行四边形的面积为 ．

    查看试题解析

  • 13. 如图，在▱ABCD中，AB=BC=5，对角线BD=8，则▱ABCD的面积为.

    查看试题解析

  • 14. 如图，在菱形ABCD中，对角线AC、BD相交于点O，且它们的长度分别为6cm和8cm，过点O的直线分别交AD、BC于点E、F，则阴影部分面积的和为cm2 ．

    查看试题解析

  • 15. 在四边形 ABCD 中，对角线 AC ， BD 交于点 O ． 现存在以下四个条件：① AB∥CD；②AO =OC；③AB =AD；④ AC 平分∠DAB ． 从中选取三个条件，可以判定四边形 ABCD为菱形． 则可以选择的条件序号是（写出所有可能的情况）．

    查看试题解析

  • 16. 点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点，对角线AC，BD交于点O，当四边形ABCD满足条件时，四边形EFGH是菱形．

    查看试题解析

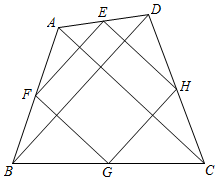
三、作图题（共8分）

  • 17. 图1，图2均为4×4的正方形网格，每个小正方形的顶点被称为格点，小正方形的边长都为1，线段AB的端点均在格点上．按要求在图1，图2中画图．

    (1)、在图1中，以线段AB为一边，画一个矩形，且使其面积为4，其余两个顶点均为格点；
    (2)、在图2中，以线段AB为对角线，画一个面积是4的菱形，且其余两个顶点均为格点．

    查看试题解析

四、解答题（共7题，共58分）

  • 18. 如图，菱形 ABCD 中， E 为对角线 BD 的延长线上一点.求证： AE=CE

    查看试题解析

  • 19. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O，过点O作直线EF⊥BD，分别交AD、BC于点E和点F，求证：四边形BEDF是菱形．

    查看试题解析

  • 20. 如图，在菱形ABCD中，对角线AC与BD相交于点O ， E为CD的中点，过点C作CF∥BD交OE的延长线于点F ， 连接DF ． 求证：四边形OCFD是矩形．

    查看试题解析

  • 21. 已知关于x的方程x2−(2m+1)x+m(m+1)=0 ．
    (1)、求证：无论m为何实数，方程总有两个不相等的实数根；
    (2)、设方程的两根分别为x1 ， x2 ， 且x1 ， x2分别是一个菱形的两条对角线长，已知菱形的面积为6，求m的值．

    查看试题解析

  • 22. 如图，将两张长为10，宽为4的矩形纸条交叉叠放，使一组对角的顶点重合，其重叠部分是四边形AGCH．

    (1)、证明：四边形AGCH是菱形；
    (2)、求菱形AGCH的周长．

    查看试题解析

  • 23. 如图，在矩形 ABCD 中， AB=15 ， BC=20 ，把边 AB 沿对角线 BD 平移，移动后的点 A' ， B' 分别对应点A，B，连接 CB' ， A'D .

    (1)、求证：四边形 A'B'CD 是平行四边形；
    (2)、当平行四边形 A'B'CD 为菱形时，求边 AB 平移的距离.

    查看试题解析

  • 24. 若一个四边形有一组邻边相等，且这组邻边夹角所对的对角线平分一个内角，则称这样的四边形为“近似菱形”．例如：如图1，在四边形ABCD中，AB＝AD，BD平分∠ABC，则四边形ABCD是近似菱形．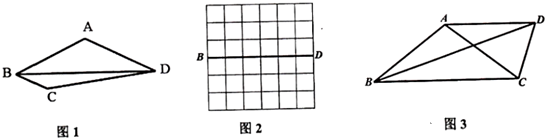 

     

    (1)、请在图2中作出一个以BD为对角线的“近似菱形”ABCD，顶点A、顶点C要在网格格点上． 
    (2)、如图3，在四边形ABCD中，AB＝AC，AD∥BC，∠CAD＝2∠DBC．求证：四边形ABCD是“近似菱形”． 
    (3)、在（2）的条件下，若BD＝3，CD＝1，求AB的长． 

    查看试题解析