2023年浙教版数学八年级下册5.1矩形 同步测试

试卷更新日期：2023-01-22 类型：同步测试

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 若矩形ABCD的邻边长分别是1，2，则BD的长是（  ）
    A、3 B、3 C、5 D、25

    查看试题解析

  • 2. 矩形的边长为10cm和15cm ， 其中一内角平分线分长边为两部分，这两部分的长为（            ）
    A、6cm和9cm  B、5cm和10cm C、4cm和11cm D、7cm和8cm

    查看试题解析

  • 3. 如图，矩形ABCD中，AC ， BD交于点O ， E ， F分别为AO ， AD的中点，若EF=4 ， AB=8 ， 则∠ACB的度数为（       ）

    A、30° B、35° C、45° D、60°

    查看试题解析

  • 4. 将6张宽为1的小长方形按如图摆放在平行四边形 ABCD 中，则平行四边形 ABCD 的面积为（    ）

    A、242 B、16+42 C、32 D、162  

    查看试题解析

  • 5. 如图，矩形ABCD中，∠BOC＝120°，BD＝12，点P是AD边上一动点，则OP的最小值为（  ）

    A、3 B、4 C、5 D、6

    查看试题解析

  • 6. 下列测量方案能判定四边形台面为矩形的是（   ）
    A、测量得出对角线相等 B、测量得出对角线互相平分 C、测量得出两组对边分别相等 D、测量得出对角线交点到四个顶点的距离相等

    查看试题解析

  • 7. 如图，在▱ABCD中，对角线AC与BD相交于点O，对于下列条件：①∠1+∠3＝90°；②BC2+CD2＝AC2；③∠1＝∠2；④AC⊥BD．能判定四边形ABCD是矩形的个数是（　　）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 8. 已知四边形ABCD是平行四边形，下列条件中能判定这个平行四边形为矩形的是（    ）
    A、∠A=∠B B、∠A=∠C C、AB=BC D、AC⊥BD

    查看试题解析

  • 9. 矩形具有而一般平行四边形不具有的性质是（  ）
    A、两组对边分别相等 B、两组对角分别相等 C、两条对角线互相平分 D、两条对角线相等

    查看试题解析

  • 10. 为了研究特殊四边形，刘老师制作了这样一个教具（如图1）：用钉子将四根木条钉成一个平行四边形框架ABCD，并在A与C，B与D两点之间分别用一根橡皮筋拉直固定，课上，刘老师右手拿住木条BC，用左手向右推动框架至AB⊥BC（如图2），观察所得到的四边形，下列结论：①∠BCA＝45°；②AC的长度变小；③AC＝BD；④AC⊥BD.正确的有（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题（每题4分，共24分）

  • 11. 一个木匠要制作矩形的踏板．他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次，就能得到矩形踏板．理由是 ．

    查看试题解析

  • 12. 如图，矩形ABCD的对角线AC与BD交于点O，过点O作OE⊥AC ， 交AD于点E，过点E作EF⊥BD ， 垂足为F，EF=1 ， OE=2 ， BD=43 ， 则矩形ABCD的面积为 ．

    查看试题解析

  • 13. 如图，在Rt△ABC中，∠BAC=90∘ ， AB=5 ， AC=12 ， P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的取值范围是 ．

    查看试题解析

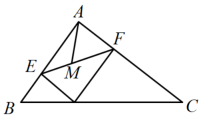  • 14. 如图，在△ABC中，D，E分别是AB，AC的中点，点F，G在边BC 上，且DF∥EG．只需添加一个条件即可证明四边形DFGE是矩形，这个条件可以是 ． （写出一个即可）

    查看试题解析

  • 15. 如图，在Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，D是AB上一动点，过点D作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是 ．

    查看试题解析

  • 16. 如图，在矩形ABCD中，点M为CD中点，将△MBC沿BM翻折至△MBE，若∠AME=15°，则∠ABE=

    查看试题解析

三、作图题（共8分）

  • 17. 如图，点A，B在方格纸的格点上，请按下列要求作图，保留作图痕迹．

    (1)、在图1中，作一个以AB为边的平行四边形，使平行四边形的顶点都在格点上．
    (2)、在图2中，作一个以AB为边的矩形，使矩形的顶点都在格点上．

    查看试题解析

四、解答题（共7题，共58分）

  • 18. 如图，四边形ABCD的对角线AC⊥BD，垂足为O，点E，F，G，H分别是AB，BC，CD，DA的中点．求证：四边形EFGH是矩形．

    查看试题解析

  • 19. 如图，两根直立的竹竿相距6m，高分别为4m和7m，求两竹竿顶端间的距离AD．

    查看试题解析

  • 20. 如图，四边形ABCD是矩形，点E在AD上，EF⊥EC交AB于点F ， 且EF=EC ， DE=2 ， 矩形的周长为16；求AE的长．

    查看试题解析

  • 21. 阅读下面材料：

    在数学课上，老师提出如下问题：

    已知：如图，在Rt△ABC中，∠ABC=90° ．

    求作：矩形ABCD ．

    小明的思考过程是：

    ①由于求作矩形，回顾了矩形的定义和判定：

    矩形的定义：有一个角是直角的平行四边形叫做矩形；

    矩形判定1：对角线相等的平行四边形是矩形；

    矩形判定2：有三个角是直角的四边形是矩形．

    ②条件给出了∠ABC=90° ， 可以选矩形的定义或者矩形判定2；经过思考，小明选择了“矩形定义”．

    ③小明决定通过作线段AC的垂直平分线，作出线段AC的中点O，再倍长线段BO ， 从而确定点D的位置．

    小明的作法如下：

    作法：①分别以点A，C为圆心，大于12AC的同样长为半径作弧，两弧分别交于点E，F；

    ③作直线EF ， 直线EF交AC于点O；

    ③作射线BO ， 在BO上截取OD ， 使得OD=OB；

    ④连接AD ， CD ．

    ∴ 四边形ABCD就是所求作的矩形．

    请你根据小明同学设计的尺规作图过程：

    (1)、使用直尺和圆规，依作法在图1中补全图形（保留作图痕迹）；
    (2)、完成下面的证明：

    证明：∵直线EF是AC的垂直平分线，

    ∴AO=OC ，

    ∵BO=DO ，

    ∴四边形ABCD是平行四边形（   ①    ）（填推理的依据）．

    ∵∠ABC=90° ，  

    ∴四边形ABCD是矩形（     ②    ）（填推理的依据）．

    (3)、参考小明的作图思路，另外设计一种作法，利用直尺和圆规在图2中完成．

    （温馨提示：保留作图痕迹，不用写作法和证明）

    查看试题解析

  • 22. 如图，已知平行四边形ABCD，延长AB到E，使 BE=AB ，连接BD，ED，EC，若 ED=AD ．

    (1)、求证： CD=BE ；
    (2)、求证：四边形BECD是矩形；
    (3)、连接AC，若 AD=7 ， CD=2 ，求AC的长．

    查看试题解析

  • 23. 如图，在矩形ABCD中，对角线AC，BD相交于点O，E，F ，G，H分别是AD，OA，BC，OC的中点.

    (1)、求证：四边形EFGH为平行四边形.
    (2)、当BC= 3 AB时，判断四边形EFGH为何种特殊四边形，并证明.

    查看试题解析

  • 24. 矩形ABCD中，AB=3，BC=4.点E，F在对角线AC上，点M，N分别在边AD，BC上.

    (1)、如图1，若AE=CF=1，M，N分别是AD，BC的中点.求证：四边形EMFN为矩形.
    (2)、如图2，若AE=CF=0.5， AM=CN=x（0<x<2） ，且四边形EMFN为矩形，求x的值.

    查看试题解析