2023年浙教版数学八年级下册第四章 平行四边形单元测试(进阶版)
试卷更新日期:2023-01-22 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 将一张五边形的纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、540° B、720° C、900° D、1080°2. 过某个多边形一个顶点的所有对角线将这个多边形分成5个三角形,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形3. 如图, 方格纸中小正方形的边长为1, , 两点在格点上,要在图中格点上找到点 ,使得 的面积为2,满足条件的点 有( )
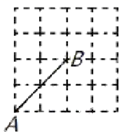 A、无数个 B、7个 C、6个 D、5个4. 如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是 , 请你找出此时的对称中心是( )
A、无数个 B、7个 C、6个 D、5个4. 如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是 , 请你找出此时的对称中心是( ) A、 B、 C、 D、5. 如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC, 以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当 时,则△AHC的面积为( )
A、 B、 C、 D、5. 如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC, 以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当 时,则△AHC的面积为( ) A、4 B、6 C、 D、6. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、7. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( )
A、4 B、6 C、 D、6. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、7. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( ) A、 B、 C、 D、8. 如图,中, , 于F,交于E,若 , 则的大小是( )
A、 B、 C、 D、8. 如图,中, , 于F,交于E,若 , 则的大小是( ) A、 B、 C、 D、9. 如图,点 是▱ 内的任意一点,连接 、 、 、 ,得到 、 、 、 ,设它们的面积分别是 、 、 、 ,给出如下结论中正确的是( )
A、 B、 C、 D、9. 如图,点 是▱ 内的任意一点,连接 、 、 、 ,得到 、 、 、 ,设它们的面积分别是 、 、 、 ,给出如下结论中正确的是( ); 如果 ,则 ; 若 ,则 ; 如果 点在对角线 上,则 : : ; 若 ,则 点一定在对角线 上.
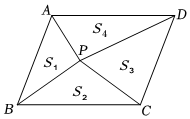 A、 B、 C、 D、10. 如图:已知 ,点 、 在线段 上且 ; 是线段 上的动点,分别以 、 为边在线段 的同侧作等边 和等边 ,连接 ,设 的中点为 ;当点 从点 运动到点 时,则点 移动路径的长是
A、 B、 C、 D、10. 如图:已知 ,点 、 在线段 上且 ; 是线段 上的动点,分别以 、 为边在线段 的同侧作等边 和等边 ,连接 ,设 的中点为 ;当点 从点 运动到点 时,则点 移动路径的长是 A、5 B、4 C、3 D、0
A、5 B、4 C、3 D、0二、填空题(每题4分,共24分)
-
11. 从一个多边形的一个顶点出发,一共可作9条对角线,则这个多边形的内角和是度.12. 在中, , , D是所在平面内的一点,以A、B、C、D为顶点的四边形是平行四边形,则的长为 .13. 已知O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .14. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 .
 15. 如图, 中, ,以AB为边在三角形外的 的对角线交于点F,AE=2,AB=5,则CF的最大值是 .
15. 如图, 中, ,以AB为边在三角形外的 的对角线交于点F,AE=2,AB=5,则CF的最大值是 .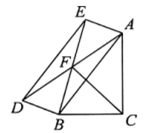 16. 如图,平行四边形ABCD的面积是20,E为AB的中点,连接OE和DE,则的面积是 .
16. 如图,平行四边形ABCD的面积是20,E为AB的中点,连接OE和DE,则的面积是 .
三、作图题(共8分)
-
17. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,点A、B均在格点上,仅用无刻度的直尺在下列网格中按要求作图.
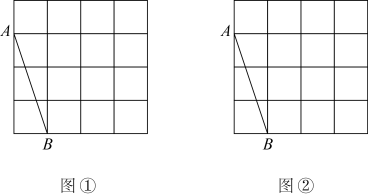 (1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.
(1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.四、解答题(共7题,共58分)
-
18. 阅读佳佳与明明的对话,解决下列问题:
 (1)、“多边形内角和为 ”,为什么不可能?(2)、佳佳求的是几边形的内角和?(3)、错当成内角和那个外角为多少度?19. 如图,平面直角坐标系中,直线 与 、 轴分别相交于点 、 .点 的坐标为 ,经过 、 作直线.
(1)、“多边形内角和为 ”,为什么不可能?(2)、佳佳求的是几边形的内角和?(3)、错当成内角和那个外角为多少度?19. 如图,平面直角坐标系中,直线 与 、 轴分别相交于点 、 .点 的坐标为 ,经过 、 作直线.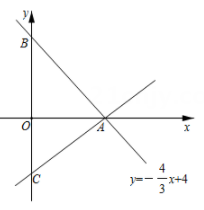 (1)、求直线 的函数表达式;(2)、若点 是直线 上的动点,点 是直线 上的动点,当以点 、 、 、 为顶点的四边形是平行四边形时,求点 的坐标.20.(1)、如图,四边形ABCD是李爷爷家的一块平行四边形田地,P为水井,现要把这块田地平均分给他的两个儿子,为了方便用水,要求两个儿子分到的地都与水井相邻,请你来设计一下,并说明你的理由。
(1)、求直线 的函数表达式;(2)、若点 是直线 上的动点,点 是直线 上的动点,当以点 、 、 、 为顶点的四边形是平行四边形时,求点 的坐标.20.(1)、如图,四边形ABCD是李爷爷家的一块平行四边形田地,P为水井,现要把这块田地平均分给他的两个儿子,为了方便用水,要求两个儿子分到的地都与水井相邻,请你来设计一下,并说明你的理由。 (2)、规律总结:回顾第13题和第14题第(1)问发现:能够平分平行四边形面积与周长的直线有条,它们的共同特点是经过的交点。21. 如图,在平面直角坐标系中,已知平行四边形的顶点为坐标原点,顶点在轴的正半轴上,在第一象限内, ,且 .
(2)、规律总结:回顾第13题和第14题第(1)问发现:能够平分平行四边形面积与周长的直线有条,它们的共同特点是经过的交点。21. 如图,在平面直角坐标系中,已知平行四边形的顶点为坐标原点,顶点在轴的正半轴上,在第一象限内, ,且 . (1)、顶点的坐标为 ,顶点的坐标为;(2)、如图2,若直线过点 , 且把平行四边形的面积分成的两部分,求直线的函数解析式;(3)、如图3,设对角线交于点 ,在轴上,有一个长为1个单位长度的可以左右平移的线段 , 点在点的左侧,连接 , 则的最小值为 .22. 如图,在▱ABCD中,对角线AC , BD相交于点O , OA=5cm , E , F为直线BD上的两个动点(点E , F始终在▱ABCD的外面),连接AE , CE , CF , AF .
(1)、顶点的坐标为 ,顶点的坐标为;(2)、如图2,若直线过点 , 且把平行四边形的面积分成的两部分,求直线的函数解析式;(3)、如图3,设对角线交于点 ,在轴上,有一个长为1个单位长度的可以左右平移的线段 , 点在点的左侧,连接 , 则的最小值为 .22. 如图,在▱ABCD中,对角线AC , BD相交于点O , OA=5cm , E , F为直线BD上的两个动点(点E , F始终在▱ABCD的外面),连接AE , CE , CF , AF . (1)、若DE= OD , BF= OB ,
(1)、若DE= OD , BF= OB ,①求证:四边形AFCE为平行四边形;
②若CA平分∠BCD , ∠AEC=60°,求四边形AFCE的周长.
(2)、若DE= OD , BF= OB , 四边形AFCE还是平行四边形吗?请写出结论并说明理由.若DE= OD , BF= OB呢?请直接写出结论.23. 在平面直角坐标系xOy中,A,B点的坐标分别为(0,4),(-4,0),P点坐标为(0,m),点E是射线BO上的动点,满足BE=1.5OP,以PE,EO为邻边作 ▱ PEOQ. (1)、当m=2时,求出PE的长度;(2)、当m>0时,是否存在m的值,使得PEOQ的面积等于△ABO面积的 , 若存在求出m的值,若不存在,请说明理由;(3)、当点Q在第四象限时,点Q关于E点的对称点为Q',点Q'刚好落在直线AB上时,求m的值(直接写出答案).24. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
(1)、当m=2时,求出PE的长度;(2)、当m>0时,是否存在m的值,使得PEOQ的面积等于△ABO面积的 , 若存在求出m的值,若不存在,请说明理由;(3)、当点Q在第四象限时,点Q关于E点的对称点为Q',点Q'刚好落在直线AB上时,求m的值(直接写出答案).24. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
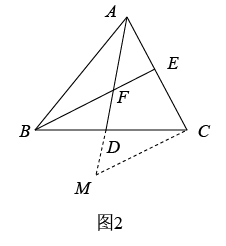

 (1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.
(1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.小明发现可以类比以上思路进行证明.
证明:如图2,延长AD至点M,使MD=FD,连接MC,……
请你根据小明的思路完成证明过程.
(2)、【方法运用】如图3,在菱形ABCD中,∠D=60°,点E为射线BC上一个动点(在点C右侧),把线段EC绕点E逆时针旋转120°得到线段BC′,连接BC′,点F是BC′的中点,连接AE、CF、EF.①请你判断线段EF和AE的数量关系是 ▲ , 并说明理由;
②若菱形ABCD的边长为6,CF=CE,请直接写出CF的长.
-