2023年浙教版数学八年级下册第四章 平行四边形 单元测试（基础版）
试卷更新日期：2023-01-22 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 一个多边形截取一个角后，形成另一个多边形的内角和是1440°，则原来多边形的边数可能是（ ）A、9，10，11 B、12，11，10 C、8，9，10 D、9，102. 如图，已知∠1+2+∠3+∠4＝280°，那么∠5的度数为（ ）
A、70° B、80° C、90° D、100°3. 如果一个多边形的每一个外角都是45°，那么这个多边形的内角和是（ ）A、540° B、720° C、1080° D、1260°4. 如图，在中， ， 点 ， 分别为 ， 的中点，则（ ）
A、 B、 C、1 D、25. 若平行四边形中两内角的度数比为2：3，则其中较小的内角是（ ）A、 B、 C、 D、6. 平行四边形不一定具有的特征是（ ）A、两组对边分别平行 B、两组对角分别相等 C、对角线相等 D、内角和为360°7. 某市实验学校的美术课上，七年级同学创造了一批民间剪纸艺术作品，下列剪纸作品中，是中心对称图形的为（ ）A、
B、
C、
D、
8. 如图，点E、F分别是▱ABCD边AD、BC的中点，G、H是对角线BD上的两点，且BG=DH．则下列结论中错误的是（ ）
A、 B、四边形EGFH是平行四边形 C、 D、9. 如图，在四边形ABCD中，ABCD，要使四边形ABCD是平行四边形，下列添加的条件错误的是（ ）
A、AB＝CD B、BC＝AD C、∠A＝∠C D、10. 在复习平行四边形的判定方法时，某同学进行了画图探究，其作法和图形如下：①如图1，作线段AC的垂直平分线，交AC于点O；②如图2，过点O作一条直线l（不过点A，C）再以点O为圆心，任意长为半径作弧，交直线l于点B，D，连接AB，BC，CD，AD．根据以上作法，不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是（ ）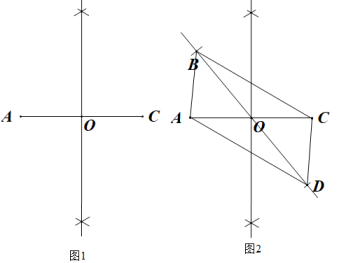
A、对角线互相平分的四边形是平行四边形 B、两组对边分别平行的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形二、填空题（每题4分，共24分）
-
11. 八边形从一个顶点出发可以引条对角线.12. 用反证法证明“在三角形中至少有一个内角大于或等于60°”，应先假设命题不成立，即三角形的三个内角都60°（填“＞”“＜”或“＝”）.13. 数学综合与实践活动课上，某兴趣小组要测定被池塘隔开的A、B两点间的距离，他们在AB外选一点C，连接AC、BC，并分别找出它们的中点D、E，连接DE．现测得 ， ， ， 则A、B两点间的距离为m．
14. 如图，平行四边形的对角线与相交于点 ， ， 垂足为 ， ， ， ， 则的长为 ．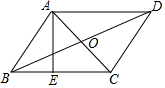
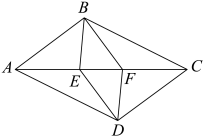
15. 在方格纸中，选择标有序号①、②、③、④中的一个小正方形涂黑，能与图中阴影部分构成中心对称图形的小正方形的序号是。
16. 已知：如图，四边形 中， ，要使四边形 为平行四边形，需添加一个条件是：.(只需填一个你认为正确的条件即可)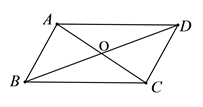
三、作图题（共8分）
-
17. 如图，方格纸中每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，的顶点均在格点上，已知点C的坐标为 ．
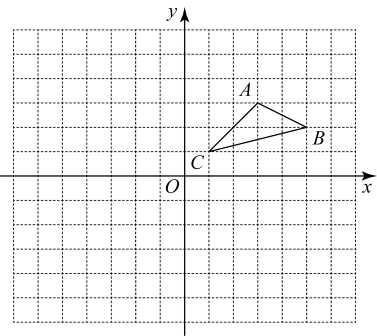(1)、画出以C为旋转中心，将按顺时针方向旋转后得到的；(2)、画出关于原点O对称的；(3)、设D为x轴上一个动点，且四边形为平行四边形，则点D坐标为 ． （直接写出答案）四、综合题（共7题，共58分）
-
18. 一个边数为 的多边形中所有对角线的条数是边数为 的多边形中所有对角线条数的6倍，求这两个多边形的边数.19. 如图，在中，点、在对角线上，且 ， 连接、 ． 求证： ， ．
20. 阅读下列文字，回答问题。题目：如图，在Rt△ABC中，∠C=90°，若∠A≠45°，则AC≠BC.
证明：假设AC=BC，
∠A≠45°，∠C=90°，∴∠A≠∠B
∴AC≠BC，这与假设矛盾，∴AC≠BC.
上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正。
21. 已知一个多边形的内角和与外角和之比为11：2。(1)、求这个多边形的内角和；(2)、求这个多边形的边数。22. 如图，在Rt△ABC中，∠ACB＝90°，D、E分别是边AC、AB的中点，连接CE、DE，过D点作DF∥CE交BC的延长线于F点．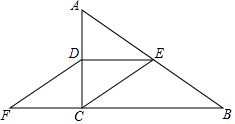
(1)、证明：四边形DECF是平行四边形；(2)、若AB＝13cm，AC＝5cm，求四边形DECF的周长．
-
