2023年浙教版数学八年级下册4.4平行四边形的判定 同步测试
试卷更新日期：2023-01-22 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 能判定四边形是平行四边形的是（ ）A、 ， B、 ， C、 ， D、 ，2. 如图四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（ ）
A、AB∥CD，∠DAC=∠BCA B、AB=CD，∠ABO=∠CDO C、AC=2AO，BD=2BO D、AO=BO，CO=DO3. 如图，在一束平行光线中插入一张对边平行的纸板，如果光线与纸板右下方所成的 ， 则光线与纸板左上方所成的的度数是（ ）
A、 B、 C、 D、4. 如图所示，在平行四边形ABCD中，AB＝3.5cm，BC＝5cm，AE平分∠BAD，CF∥AE，则AF的长度是（ ）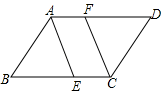
A、1.5cm B、2.5cm C、3.5cm D、0.5cm5. 如图，在中， ， ， 、、分别为、、的中点，连接、 ， 则四边形的周长是（ ）
A、5 B、7 C、9 D、116. 下列四组条件中，能判定四边形ABCD是平行四边形的有（ ）①AB=CD，AD=BC②AB=CD，ABCD ③AB=CD，ADBC④ABCD，ADBC
A、②③④ B、①②④ C、①②③ D、①③④7. 如图1，直线 ， 直线分别交直线 ， 于点A，B．小嘉在图1的基础上进行尺规作图，得到如图2，并探究得到下面两个结论：①四边形ABCD是邻边不相等的平行四边形；②四边形ABCD是对角线互相垂直的平行四边形．下列判断正确的是（ ）
A、①②都正确 B、①错误，②正确 C、①②都错误 D、①正确，②错误8. 如图，已知△ABC是边长为3的等边三角形，点D是边BC上的一点，且BD＝1，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则下列结论中①△ABD≌△BCF；②四边形BDEF是平行四边形；③S四边形BDEF；④S△AEF ． 其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个9. 如图，我们称四个顶点都恰好在格点的四边形为格点四边形，A，B为4×4的正方形网格中的两个格点，在此图中以A，B为顶点的格点四边形是平行四边形的个数是（ ）．
A、10 B、11 C、12 D、1310. 如图1，中， ， 为锐角．要在对角线上找点 ， ， 使四边形为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案（ ）
A、甲、乙、丙都是 B、只有甲、乙才是 C、只有甲、丙才是 D、只有乙、丙才是二、填空题（每题4分，共24分）
-
11. 在四边形ABCD中， ， ， 若 ， 则.12. 如图两张长相等，宽分别是1和3的矩形纸片上叠合在一起，重叠部分为四边形ABCD，且AB+BC＝6，则四边形ABCD的面积为 ．
13. 如图，已知△ABC中，D，E分别是AB，AC的中点，连接DE并延长至F．使EF＝DE，连接CF．若∠B＝45°，则的度数为 ．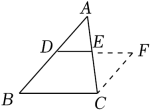
14. 如图所示的网格是正方形网格，点A，B，C，D是网格线交点，则△ABC的面积与△BCD的面积的大小关系为：S△ABCS△BCD（填“＞”，“＝”或“＜”）．
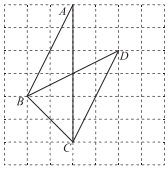15. 如图，已知（ ， 且），在的两边上各任取一点，分别记为 ， 过该两点分别引一条直线，并使得该直线与所在的边夹角也为 ， 设两条直线交于点O，则的数量应是.
16. 如图所示，在▱ABCD中，对角线交于点O，点E，F在对角线AC上（不同于点A，C），当点E，F的位置满足的条件时，四边形DEBF是平行四边形。
三、作图题（共8分）
-
17. 如图，在10×10的正方形网格中（每个正方形的边长为1），点A和点B都在格点上，仅用无刻度的直尺 ， 分别按以下要求作图．
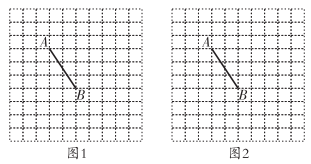(1)、图1中，以AB为边作一平行四边形，要求顶点都在格点上，且其面积为6；(2)、图2中，以AB为对角线作一平行四边形，要求顶点都在格点上，且其面积为10．四、解答题（共7题，共58分）
-
18. 如图所示，在▱中，点 ， 是对角线上的两点，且 ， 连接 ， ， ， 求证：四边形是平行四边形．
19. 如图所示，已知点在平行四边形的对角线上，且 ， 连接 ， .求证：四边形是平行四边形.
20. 先阅读下列材料，再解答问题．尺规作图：
已知： ， D是边上一点，如图1．
求作：四边形 ， 使得四边形是平行四边形．
小明的做法如下：
⑴设计方案
先一个正确的草图，如图2，
再分析实现目标的具体方法．
⑵设计作图步骤，完成作图
作法：如图3，
①以点C为圆心、为半径画弧；
②再以点D为圆心、为半径画弧，两弧交于点F；
③连接与 ．
∴四边形即为所求．
请在图3中完成尺规作图，保留作图痕迹
⑶推理论证
证明：∵ ，
∴四边形DBCF是平行四边形．（ ）（填推理依据）
21. 已知点E、F分别是▱ABCD的边BC、AD的中点．
(1)、求证：四边形AECF是平行四边形；(2)、若BC＝12，∠BAC＝90°，求▱AECF的周长．22. 如图，在△ABC中，D是BC边的中点，分别过点B、C作射线AD的垂线，垂足分别为E、F，连接BF、CE.
(1)、求证：四边形BECF是平行四边形；(2)、若AF＝FD，在不添加辅助线的条件下，直接写出与△ABD面积相等的所有三角形.23. 如图，平行四边形ABCD，AD＝AC，AD⊥AC.
(1)、如图1，点E在AD延长线上，CE∥BD，求证：点D为AE中点；(2)、如图2，点E在AB中点，F是AC延长线上一点，且ED⊥EF，求证：ED＝EF；(3)、在（2）的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形？并证明你的结论（先补全图形再解答）.24. 如图，在平面直角坐标系中，点A，B的坐标分别是（﹣4，0），（0，8），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造▱PCOD，在线段OP延长线上取点E，使PE＝AO，设点P运动的时间为t秒．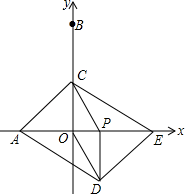
(1)、当点C运动到线段OB的中点时，求t的值及点E的坐标；(2)、当点C在线段OB上时，求证：四边形ADEC为平行四边形；(3)、在线段PE上取点F，使PF＝3，过点F作MN⊥PE，截取FM＝ ，FN＝1，且点M，N分别在第一、四象限，在运动过程中，当点M，N中，有一点落在四边形ADEC的边上时，直接写出所有满足条件的t的值．
-