2023年浙教版数学八年级下册4.5三角形中位线 同步测试
试卷更新日期:2023-01-22 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,在 中, 分别是 的中点, 分别是 的中点,且 ,则的长度是( )
 A、 B、 C、 D、2. 如图,在中, , 平分交于点D,点F在上,且 , 连接 , E为的中点,连接 , 则的长为( )
A、 B、 C、 D、2. 如图,在中, , 平分交于点D,点F在上,且 , 连接 , E为的中点,连接 , 则的长为( ) A、2 B、3 C、4 D、53. 如图,▱ABCD的对角线AC,BD交于点O,E是AD的中点,连结OE,AC=8,BC=10,若AC⊥CD,则OE等于( )
A、2 B、3 C、4 D、53. 如图,▱ABCD的对角线AC,BD交于点O,E是AD的中点,连结OE,AC=8,BC=10,若AC⊥CD,则OE等于( ) A、3 B、4 C、5 D、64. 如图,为了测量池塘边、两地之间的距离,在线段的同侧取一点 , 连结并延长至点 , 连结并延长至点 , 使得、分别是、的中点,若 , 则线段的长度是( )
A、3 B、4 C、5 D、64. 如图,为了测量池塘边、两地之间的距离,在线段的同侧取一点 , 连结并延长至点 , 连结并延长至点 , 使得、分别是、的中点,若 , 则线段的长度是( ) A、 B、 C、 D、5. 如图,平行四边形中,对角线相交于点 , 点E是的中点,则与的面积比为( )
A、 B、 C、 D、5. 如图,平行四边形中,对角线相交于点 , 点E是的中点,则与的面积比为( )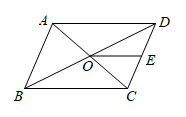 A、1:2 B、1:3 C、1:4 D、1:56. 如图,是内一点, , , , , , , , 分别是 , , , 的中点,则四边形的周长为( )
A、1:2 B、1:3 C、1:4 D、1:56. 如图,是内一点, , , , , , , , 分别是 , , , 的中点,则四边形的周长为( ) A、20 B、24 C、36 D、417. 如图,▱的对角线 , 相交于点 , , , 则▱的周长为( )
A、20 B、24 C、36 D、417. 如图,▱的对角线 , 相交于点 , , , 则▱的周长为( ) A、5 B、10 C、15 D、208. 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠CBD=30°,∠ADB=100°,则∠PFE的度数是( )
A、5 B、10 C、15 D、208. 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠CBD=30°,∠ADB=100°,则∠PFE的度数是( ) A、15° B、25° C、30° D、35°9. 如图,在平行四边形中,O为对角线的中点, , 点E为中点,并且 , 则的度数是( )
A、15° B、25° C、30° D、35°9. 如图,在平行四边形中,O为对角线的中点, , 点E为中点,并且 , 则的度数是( ) A、 B、 C、 D、10. 如图,在证明三角形的中位线定理时,小兰首先将原图形上面的三角形部分剪开,并旋转180°拼到下方.类似地,现有如图所示的四边形ABCD, , 若 , , E、F分别是AB和DC的中点,则( )
A、 B、 C、 D、10. 如图,在证明三角形的中位线定理时,小兰首先将原图形上面的三角形部分剪开,并旋转180°拼到下方.类似地,现有如图所示的四边形ABCD, , 若 , , E、F分别是AB和DC的中点,则( ) A、4 B、4.5 C、5 D、6
A、4 B、4.5 C、5 D、6二、填空题(每题4分,共24分)
-
11. 三角形的三条中位线的长分别是3,4,5,则这个三角形的周长是 .12. 在△ABC中,∠C=90°,BC=6,AC=8,顺次连接△ABC各边中点,得到的三角形面积是 .13. △ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED= .
 14. 如图,在平行四边形中,对角线 , 相交于点O,在的延长线上取点E,使 , 连接交于点F,若 , 则 .
14. 如图,在平行四边形中,对角线 , 相交于点O,在的延长线上取点E,使 , 连接交于点F,若 , 则 . 15. 如图, , 是四边形的对角线,点E,F分别是 , 的中点,点M,N分别是 , 的中点,顺次连接 , , , , 若 , 则四边形的周长是 .
15. 如图, , 是四边形的对角线,点E,F分别是 , 的中点,点M,N分别是 , 的中点,顺次连接 , , , , 若 , 则四边形的周长是 . 16. 如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是 .
16. 如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是 .
三、作图题(共8分)
-
17. 如图,在 中,点 为 边的中点,请用尺规在 边上求作点 ,使得 .(保留作图痕迹,不写作法)

四、解答题(共7题,共58分)
-
18. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之.
 19. 如图,在 中, , , 分别是边 , 的中点, 在 的延长线上, .求证: .
19. 如图,在 中, , , 分别是边 , 的中点, 在 的延长线上, .求证: . 20. 如图,△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE.
20. 如图,△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE. (1)、求证:四边形BCFD是平行四边形.(2)、当AB=BC时,若BD=2,BE=3,求AC的长.21. 如图,在▱ 中,点 , 分别是 , 的中点,点 , 在对角线 上,且 .
(1)、求证:四边形BCFD是平行四边形.(2)、当AB=BC时,若BD=2,BE=3,求AC的长.21. 如图,在▱ 中,点 , 分别是 , 的中点,点 , 在对角线 上,且 .
 (1)、求证:四边形 是平行四边形;(2)、连接 交 于点 ,若 , ,求 的长.22. 如图,在Rt△ABC中,∠ACB=90°,点D是AB上一点,连接CD,∠ADC+∠DCB=90°,AE平分∠CAB交CD于点E.
(1)、求证:四边形 是平行四边形;(2)、连接 交 于点 ,若 , ,求 的长.22. 如图,在Rt△ABC中,∠ACB=90°,点D是AB上一点,连接CD,∠ADC+∠DCB=90°,AE平分∠CAB交CD于点E. (1)、求证:AE垂直平分CD;(2)、若AC=6,BC=8,点F为BC的中点,连接EF,求EF的长.23. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
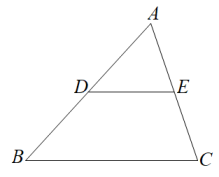
(1)、求证:AE垂直平分CD;(2)、若AC=6,BC=8,点F为BC的中点,连接EF,求EF的长.23. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.已知:如图,中,D、E分别是的中点.
求证:∥ , 且 .

方法一
证明:如图,延长至点F,使 , 连接 .

方法二
证明:如图,过点C作∥交的延长线于F.
 24. 如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A,B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,P从O出发以每秒3个单位长度的速度向终点B运动,Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒).
24. 如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A,B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,P从O出发以每秒3个单位长度的速度向终点B运动,Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒). (1)、求线段AB的长,及点A的坐标;
(1)、求线段AB的长,及点A的坐标;
(2)、t为何值时,△BPQ的面积为2 ;(3)、若C为OA的中点,连接QC,QP,以QC,QP为邻边作平行四边形PQCD,①t为何值时,点D恰好落在坐标轴上;
②是否存在时间t使x轴恰好将平行四边形PQCD的面积分成1:3的两部分,若存在,直接写出t的值.
-