2023年浙教版数学八年级下册第三章 数据分析初步 单元测试（基础版）
试卷更新日期：2023-01-22 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 某校八年2班5位同学的身高（单位：）组成一组数据为：170、169、172、173、171，则这5位同学身高的平均值（ ）A、170 B、171 C、171.5 D、1722. 某学校在开展“生活垃圾分类星级家庭”评选活动中，从八年级任选出10名同学汇报了各自家庭1天生活垃圾收集情况，将有关数据整理如下表：
生活垃圾收集量（单位：kg）
0.5
1
1.5
2
同学数（人）
2
3
4
1
请你计算每名同学家庭平均1天生活垃圾收集量是（ ）
A、0.9kg B、1kg C、1.2kg D、1.8kg3. 希望中学规定学生的学期体育成绩满分为 ， 其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%若小强的三项成绩百分制依次是95，90，91则小强这学期的体育成绩是（ ）A、92 B、91.5 C、91 D、904. 家乐福超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如表：测试项目
创新能力
综合知识
语言表达
测试成绩（分数）
70
80
92
将创新能力、综合知识和语言表达三项测试成绩技5：3：2的比树计入总成绩，测该应聘者的总成绩是（ ）分．
A、77.4 B、80 C、92 D、以上都不对5. 在射击训练中，某队员的10次射击成绩如图，则这10次成绩的中位数和众数分别是（ ）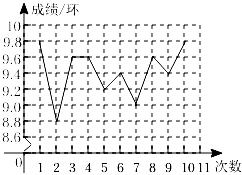
A、9.3，9.6 B、9.5，9.4 C、9.5，9.6 D、9.6，9.86. 期末考试后，办公室里有两位数学老师正在讨论他们班的数学考试成绩，邱老师：“我班的学生考得还不错，有一半的学生考90分以上，一半的学生考不到90分，”张老师：“我班大部分的学生都考在85分到90分之间，“依照上面两位老师所叙述的话你认为邱者师、张者师所说的话分别针对（ ）A、平均数、众数 B、中位数、众数 C、中位数、方差 D、平均数、中位数7. 颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩（以“次”为单位计）为：52，50，46，54，50，56，47，52，53，50．则以下数据中计算错误的是（ ）A、平均数为51 B、方差为8.4 C、中位数为53 D、众数为508. 已知一组数据的方差是3，则这组数据的标准差是（ ）A、 B、3 C、 D、99. 甲、乙两名运动员在相同的条件下，各射击10次，经过计算，甲、乙两人成绩的平均数均是9.5环，甲的成绩的方差是0.125，乙的成绩的方差是1.85，那么这10次射击中，甲、乙成绩的稳定情况是（ ）A、甲较为稳定 B、乙较为稳定 C、两个人成绩一样稳定 D、不能确定10. 甲、乙、丙、丁四地去年同期的平均气温 （单位： ）和方差 （单位： ）如下表．根据表中数据， 要从中选取一处气温低且稳定的地区举办高山滑雪比赛，应选择（ ）甲
乙
丙
丁
-2
-2
0
-1
3
0.8
1.6
0.8
A、甲 B、乙 C、丙 D、丁二、填空题（每题4分，共24分）
-
11. 小聪这学期的数学平时成绩90分，期中考试成绩80分，期末考试成绩82分，那么，小聪这学期数学平均成绩为分；若计算总评成绩的方法如下：平时成绩∶期中成绩∶期末成绩=3∶3∶4，则小聪总评成绩是分．12. 某市在一次空气污染指数抽查中，收集到10人的数据如下，61，75.81，56，81，91，92，91，75，81．该组数据的众数是 ．13. 某校男子足球队的年龄分布如条形图所示，则这些队员年龄的中位数是 ．
14. 已知一组数据：2，3，4，5，6，则这组数据的标准差是 .15. 若四个数据4，5，x，6的平均数是5，那么x的值是 ．16. 如表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差，根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择 ．甲
乙
丙
丁
平均数（环）
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6
三、解答题（共8题，共66分）
-
17. 在校园诗歌朗诵比赛中，采用10位评委现场打分，每位选手的最后得分为去掉一个最低分，去掉一个最高分后的平均分，已知10位评委给某位选手的打分分别是：9.0 9.4 9.3 9.8 9.5 9.1 9.6 9.4 9.7 9.6
求这位选手的最后得分．
18. 某农业科技部门为了解甲、乙两种新品西瓜的品质（大小、甜度等），进行了抽样调查，在相同条件下，随机抽取了两种西瓜各7份样品，对西瓜的品质进行评分（百分制），并对数据进行收集、整理，得到两种西瓜得分的统计图：
对数据进行分析，得到如下统计量：
平均数
中位数
众数
方差
甲种西瓜
88
88
96
44.86
乙种西瓜
88
90
90
21.43
请根据以上信息分析哪种西瓜的品质更好，并说明理由.
19. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图，请判断甲、乙两名射击运动员中谁的成绩的方差小，并计算其方差.
20. 某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务，这两家厂生产的皮具款式和材料都符合要求，因此只需要检测皮具质量的克数是否稳定.现从两家提供的样品中各抽查10件，测得它们的质量如下（单位：克）甲：500，499，500，500，503，498，497，502，500，501，
乙：499，500，498，501，500，501，500，499，500，502
你认为该选择哪一家制造厂？
21. 为了解学生零花钱的使用情况，校团委随机调查了本校部分学生每人一周的零花钱数额，并绘制了如图甲、乙所示的两个统计图（部分未完成）．请根据图中信息，回答下列问题：
(1)、校团委随机调查的学生人数是 ▲ ， 请你补全条形统计图；(2)、表示“50元”的扇形所占百分数是 ，(3)、求被调查的学生每人一周零花钱数额的平均数．22. 某中学在一次爱心捐款活动中，全体同学积极踊跃捐款．现随机抽查了八年级20位同学捐款情况，并绘制出如下的统计表和统计图．根据上述信息，回答下列问题：捐款（元）
20
50
100
150
200
人数（人）
4
8
2
1
(1)、 ， ；(2)、学生捐款数目的众数是元，中位数是元，平均数是元；(3)、若该校有学生1500人，估计该校学生共捐款多少元？23. 某中学八年级甲、乙两班分别选5名同学参加“防疫宣传”演讲比赛，其预赛成绩（单位：分）如图所示：
根据以上信息，解答下列问题
(1)、求出表中的a、b、c、d平均数
中位数
众数
方差
甲班
8.5
b
8.5
d
乙班
a
8
c
1.6
(2)、请你任选一组统计量描述两个班的成绩水平(3)、乙班小明说：“我的成绩在我们班是中等水平”，你知道他是几号选手吗?24. 某中学举行“书香进校园”知识竞赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩（满分为100分）如图所示．
平均数
中位数
众数
初中部
85
85
高中部
85
(1)、根据图示填写表格；(2)、结合两学部决赛成绩的平均数和中位数，分析哪个学部的决赛成绩较好．(3)、如果规定选手成绩较稳定的学部胜出，你认为哪个学部能胜出？请说明理由．