2023年中考数学复习考点一遍过——反比例函数

试卷更新日期：2023-01-19 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列函数是y关于x的反比例函数的是（）

A、y＝ $\frac{1}{x + 1}$ B、y＝ $\frac{1}{x^{2}}$ C、y＝- $\frac{1}{2 x}$ D、y＝- $\frac{x}{2}$

查看试题解析
2. 如果点P（1，2）在双曲线y＝ $\frac{k}{x}$ 上，那么 $k$ 的值是（）

A、-4 B、4 C、2 D、-2

查看试题解析
3. 关于反比例函数y＝ $\frac{1}{x}$ ，下列说法不正确的是（）

A、函数图象分别位于第二、四象限 B、函数图象关于原点成中心对称 C、函数图象经过点（1，1） D、当x＞0时，y随x的增大而减小

查看试题解析
4. 如图，A为反比例函数 $y = \frac{k}{x}$ 的图象上一点，AB垂直x轴于B，若 $S_{Δ A O B} = 2$ ，则k的值为（）

A、4 B、2 C、-2 D、1

查看试题解析
5. 若点 $A (- 1 ， y_{1}) ， B (1 ， y_{2}) ， C (3 ， y_{3})$ 在反比例函数 $y = \frac{9}{x}$ 的图像上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

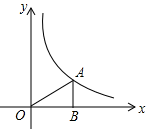A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
6. 如图，矩形ABCD的顶点A、C分别在x、y轴的正半轴上，点D（-2，3），AD＝5，若反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点B，则k的值为（）

A、4 B、 $\frac{16}{3}$ C、10 D、 $\frac{32}{2}$

查看试题解析
7. 如图，正比例函数 $y = k_{1} x$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于 $A (1 ， m)$ 、B两点，当 $k_{1} x \leq \frac{k_{2}}{x}$ 时，x的取值范围是（）

A、 $- 1 \leq x < 0$ 或 $x ≥ 1$ B、 $x \leq - 1$ 或 $0 < x \leq 1$ C、 $x \leq - 1$ 或 $x ≥ 1$ D、 $- 1 \leq x < 0$ 或 $0 < x \leq 1$

查看试题解析
8. 在同一平面直角坐标系中，反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = k x - k$ （ $k$ 为常数，且 $k \neq 0$ ）的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 某电子产品的售价为8000元，购买该产品时可分期付款：前期付款3000元，后期每个月分别付相同的数额，则每个月付款额y（元）与付款月数x（x为正整数）之间的函数关系式是（）

A、 $y = \frac{8000}{x} - 3000$ B、 $y = \frac{8000}{x} + 3000$ C、 $y = \frac{3000}{x}$ D、 $y = \frac{5000}{x}$

查看试题解析
10. 如图，在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交矩形 $O A B C$ 的边 $A B$ 于点 $M (1 ， 3)$ ，交边 $B C$ 于点N，若点B关于直线 $M N$ 的对称点 $B^{'}$ 恰好在x轴上，则 $O C$ 的长为（）

A、4 B、 $3 \sqrt{3} - 1$ C、 $\sqrt{10} + 1$ D、 $\sqrt{5} + 2$

查看试题解析

二、填空题（每题3分，共24分）

11. 反比例函数 $y = - \frac{6}{x}$ 的图像上有三点 $(- 3 ， y_{1})$ ， $(1 ， y_{2})$ ， $(6 ， y_{3})$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是.

查看试题解析
12. 如图，等腰 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 8$ ，点B在y轴上， $B C ∥ x$ 轴，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图像经过点A，交 $B C$ 于点D，若 $A B = B D$ ，则k的值为.

查看试题解析
13. 如图，点A、B分别在反比例函数 $y = \frac{1}{x} (x > 0)$ 、 $y = \frac{k}{x} (x > 0)$ 的图象上，且 $∠ A O B = 90 °$ ， $s i n B = \frac{1}{2}$ ，则 $k =$

查看试题解析
14. 如图，正比例函数 $y = x$ 与反比例函数 $y = \frac{1}{x}$ 的图像相交于A、C两点， $A B ⊥ x$ 轴于B， $C D ⊥ x$ 轴于D，则四边形 $A B C D$ 面积为.

查看试题解析
15. 如图，点A是射线 $y = k_{1} x (x \geq 0)$ 上一点，过点A作 $A B ⊥ x$ 轴于点B，以 $A B$ 为边在其右侧作正方形 $A B C D$ ，过点A的双曲线 $y = \frac{k_{2}}{x}$ 交 $C D$ 边于点E，若 $\frac{D E}{E C} = \frac{3}{2}$ ，则 $k_{1}$ 的值是．

查看试题解析
16. 如图，在反比例函数 $y = \frac{2}{3 x}$ 的图像上有一动点A，连接AO并延长交图像的另一分支于点B，在第四象限内有一点C，满足AC=BC，当点A运动时，点C始终在函数 $y = \frac{k}{x}$ 的图像上运动，若 $t a n ∠ C A B = 3$ ，则k的值为．

查看试题解析
17. 在平面直角坐标系中，点 $A (- 2 ， 1)$ 为直线 $y = k x$ $(k \neq 0)$ 和双曲线 $y = \frac{m}{x}$ $(m \neq 0)$ 的一个交点，点B在 $x$ 轴负半轴上，且点B到 $y$ 轴的距离为3，如果在直线 $y = k x$ $(k \neq 0)$ 上有一点 $P$ ，使得 $S_{Δ A B P} = 2 S_{Δ A B O}$ ，那么点 $P$ 的坐标是．

查看试题解析
18. 在平面直角坐标系中，将点 $A (2 ， 3)$ 向下平移5个单位长度得到点 $B$ ，若点 $B$ 恰好在反比例函数 $y = \frac{k}{x}$ 的图象上，则 $k$ 的值是.

查看试题解析

三、解答题（共8题，共66分）

19. 已知 $y = y_{1} + y_{\begin{array}{l} 2 \end{array}}$ ，其中 $y_{1}$ 与 $x$ 成反比例， $y_{2}$ 与 $2 x + 1$ 成正比，且当 $x = 1$ 时 $， y = 11$ ；当 $x = - 1$ 时， $y = - 5$ ，求 $y$ 关于 $x$ 的函数解析式．

查看试题解析
20. 如图，一次函数 $y = x - 2$ 的图象与反比例函数 $y = \frac{3}{x}$ 的图象交于A、B两点，求 $△ O A B$ 的面积.

查看试题解析
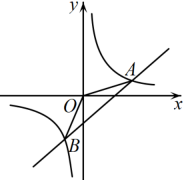21. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $A (- 2 ， 1)$ ， $B (1 ， n)$ 两点.

$($ Ⅰ $)$ 试确定上述反比例函数和一次函数的表达式；

$($ Ⅱ $)$ 连OB，在x轴上取点C，使 $B C = B O$ ，并求 $△ O B C$ 的面积；

$($ Ⅲ $)$ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.

查看试题解析
22. 如图，在平面直角坐标系中，四边形OABC为矩形，点D为AB的中点．一次函数y＝﹣3x+6的图象经过点C、D，反比例函数y＝ $\frac{k}{x}$ （x＞0），求k的值．

查看试题解析
23. 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在函数y=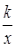（k>0，x>0）的图象上，点D的坐标为（4，3）.

(1)、求k的值；

(2)、若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y= $\frac{k}{x}$ （k>0，x>0）的图象上时，求菱形ABCD沿x轴正方向平移的距离.

查看试题解析
24. 某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y（℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题：

(1)、求这天的温度y与时间x（0≤x≤24）的函数关系式；

(2)、恒温系统设定的恒定温度为；

(3)、若大棚内的温度低于10℃时，蔬菜会受到伤害.问这天内，为避免蔬菜受到伤害，恒温系统最多可以关闭多少小时？

查看试题解析
25. 如图，一次函数 $y = k x + 2$ 的图像与 $x$ 轴、 $y$ 轴分别相交于 $A$ ， $B$ 两点，且与反比例函数 $y = \frac{n}{x} (n \neq 0)$ 的图像在第一象限交于点 $C$ ，若 $O A = O B$ ， $B$ 是线段 $A C$ 的中点．

(1)、求一次函数和反比例函数的解析式．

(2)、直接写出不等式 $k x + 2 < \frac{n}{x}$ 的解集．

查看试题解析
26. 如图，已知在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图像经过点A、 $B (- 1 ， 0)$ ，反比例函数 $y = \frac{6}{x}$ 的图像也经过点A，且点A横坐标是2．

(1)、求一次函数的解析式．

(2)、点C是x轴正半轴上的一点，连接 $A C$ ， $t a n ∠ A C B = \frac{3}{4}$ ，过点C作 $C E ⊥ x$ 轴分别交反比例函数 $y = \frac{6}{x}$ 和一次函数 $y = k x + b (k \neq 0)$ 的图像于点D、E，求点D、E的坐标．

(3)、在（2）的条件下，连接 $A D$ ，一次函数 $y = k x + b (k \neq 0)$ 的图像上是否存在一点F使得 $△ E A D$ 和 $△ E C F$ 相似？若存在，请直接写出点F坐标；若不存在，请说明理由．

查看试题解析