2023年中考数学精选真题实战测试27 图形的基础知识 A
试卷更新日期:2023-01-18 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
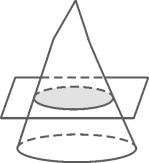 A、
A、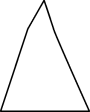 B、
B、 C、
C、 D、
D、 2. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
2. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )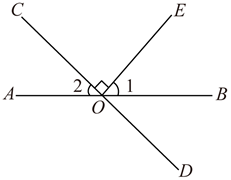 A、26° B、36° C、44° D、54°3. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A、26° B、36° C、44° D、54°3. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A、
A、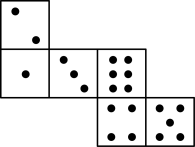 B、
B、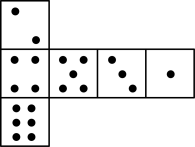 C、
C、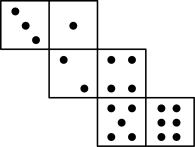 D、
D、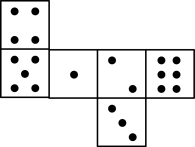 4. 如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
4. 如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )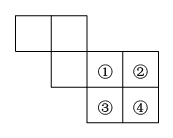 A、① B、② C、③ D、④5. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )
A、① B、② C、③ D、④5. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )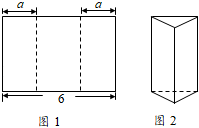 A、1 B、2 C、3 D、46. 如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A、1 B、2 C、3 D、46. 如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )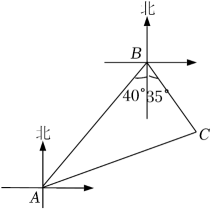 A、北偏东70° B、北偏东75° C、南偏西70° D、南偏西20°7. 互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )A、点A在B、C两点之间 B、点B在A、C两点之间 C、点C在A、B两点之间 D、无法确定8. 已知∠α=25°30′,则它的余角为( )A、25°30′ B、64°30′ C、74°30′ D、154°30′9. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )
A、北偏东70° B、北偏东75° C、南偏西70° D、南偏西20°7. 互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )A、点A在B、C两点之间 B、点B在A、C两点之间 C、点C在A、B两点之间 D、无法确定8. 已知∠α=25°30′,则它的余角为( )A、25°30′ B、64°30′ C、74°30′ D、154°30′9. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )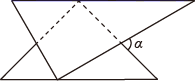 A、45° B、60° C、75° D、85°10. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )
A、45° B、60° C、75° D、85°10. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )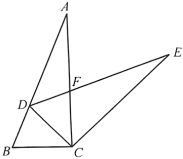 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为
 12. 如图,PA,PB表示以P为起点的两条公路,其中公路PA的走向是南偏西34 , 公路PB的走向是南偏东56 , 则这两条公路的夹角∠APB=°.
12. 如图,PA,PB表示以P为起点的两条公路,其中公路PA的走向是南偏西34 , 公路PB的走向是南偏东56 , 则这两条公路的夹角∠APB=°.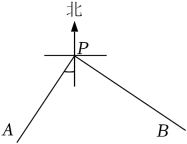 13. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
13. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).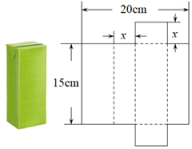 14. 图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若 ,则BC长为cm(结果保留根号).
14. 图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若 ,则BC长为cm(结果保留根号).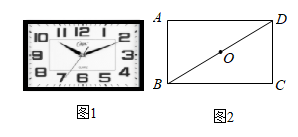 15. 下图是可调躺椅示意图(数据如图), 与 的交点为 ,且 , , 保持不变.为了舒适,需调整 的大小,使 ,则图中 应(填“增加”或“减少”)度.
15. 下图是可调躺椅示意图(数据如图), 与 的交点为 ,且 , , 保持不变.为了舒适,需调整 的大小,使 ,则图中 应(填“增加”或“减少”)度.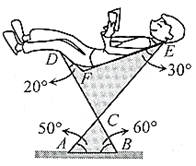 16. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿方向航行.
16. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿方向航行.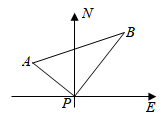
三、解答题(共7题,共72分)
-
17. 在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
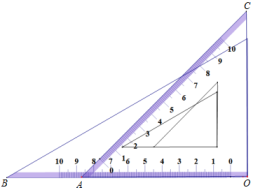
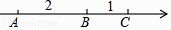 (1)、若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?(2)、若原点O在图中数轴上点C的右边,且CO=28,求p.18. 1厘米为1个单位长度用直尺画数轴时,数轴上互为相反数的点A和点B刚好对着直尺上的刻度2和刻度8
(1)、若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?(2)、若原点O在图中数轴上点C的右边,且CO=28,求p.18. 1厘米为1个单位长度用直尺画数轴时,数轴上互为相反数的点A和点B刚好对着直尺上的刻度2和刻度8 (1)、写出点A和点B表示的数;(2)、写出与点B距离为9.5厘米的直尺左端点C表示的数;(3)、在数轴上有一点D,其到A的距离为2,到B的距离为4,求点D关于原点点对称的点表示的数.19. 有两张长12cm,宽10cm的矩形纸板,分别按照图1与图2两种方式裁去若干小正方形和小矩形,剩余部分(阴影部分)恰好做成无盖和有盖的长方体纸盒各一个.
(1)、写出点A和点B表示的数;(2)、写出与点B距离为9.5厘米的直尺左端点C表示的数;(3)、在数轴上有一点D,其到A的距离为2,到B的距离为4,求点D关于原点点对称的点表示的数.19. 有两张长12cm,宽10cm的矩形纸板,分别按照图1与图2两种方式裁去若干小正方形和小矩形,剩余部分(阴影部分)恰好做成无盖和有盖的长方体纸盒各一个.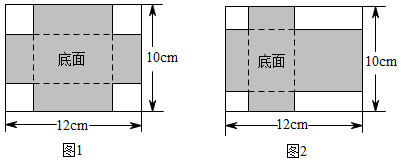 (1)、做成有盖长方体纸盒的裁剪方式是(填“图1”或“图2”).(2)、已知图1中裁去的小正方形边长为1.5cm,求做成的纸盒的底面积.(3)、已知按图2裁剪方式做成纸盒的底面积为24cm2 , 则剪去的小正方形的边长为多少cm?20. 如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)、做成有盖长方体纸盒的裁剪方式是(填“图1”或“图2”).(2)、已知图1中裁去的小正方形边长为1.5cm,求做成的纸盒的底面积.(3)、已知按图2裁剪方式做成纸盒的底面积为24cm2 , 则剪去的小正方形的边长为多少cm?20. 如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
 21. 已知数轴上有两个点A:-3,B:1.
21. 已知数轴上有两个点A:-3,B:1.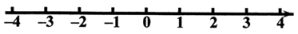 (1)、求线段AB的长;(2)、若 , 且m<0;在点B右侧且到点B距离为5的点表示的数为n.
(1)、求线段AB的长;(2)、若 , 且m<0;在点B右侧且到点B距离为5的点表示的数为n.①求m与n;
②计算2m+n+mn;
22.(1)、(算一算)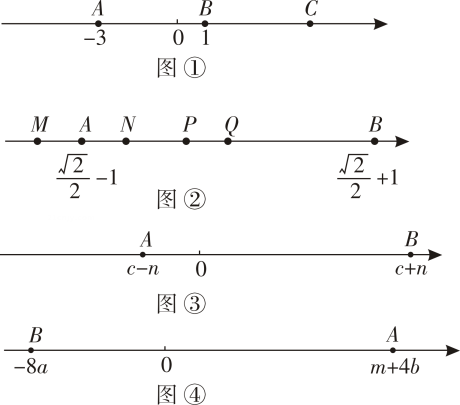
如图①,点A、B、C在数轴上,B为AC的中点,点A表示﹣3,点B表示1,则点C表示的数为 , AC长等于;
(2)、(找一找)如图②,点M、N、P、Q中的一点是数轴的原点,点A、B分别表示实数 ﹣1、 +1,Q是AB的中点,则点是这个数轴的原点;
(3)、(画一画)如图③,点A、B分别表示实数c﹣n、c+n,在这个数轴上作出表示实数n的点E(要求:尺规作图,不写作法,保留作图痕迹);
(4)、(用一用)学校设置了若干个测温通道,学生进校都应测量体温,已知每个测温通道每分钟可检测a个学生.凌老师提出了这样的问题:假设现在校门口有m个学生,每分钟又有b个学生到达校门口.如果开放3个通道,那么用4分钟可使校门口的学生全部进校;如果开放4个通道,那么用2分钟可使校门口的学生全部进校.在这些条件下,a、m、b会有怎样的数量关系呢?
爱思考的小华想到了数轴,如图④,他将4分钟内需要进校的人数m+4b记作+(m+4b),用点A表示;将2分钟内由4个开放通道检测后进校的人数,即校门口减少的人数8a记作﹣8a,用点B表示.
①用圆规在小华画的数轴上分别画出表示+(m+2b)、﹣12a的点F、G,并写出+(m+2b)的实际意义;
②写出a、m的数量关系.
23. 数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.(1)、探究一:求不等式|x﹣1|<2的解集探究|x﹣1|的几何意义
如图①,在以O为原点的数轴上,设点A′对应的数是x﹣1,由绝对值的定义可知,点A′与点O的距离为|x﹣1|,可记为A′O=|x﹣1|.将线段A′O向右平移1个单位得到线段AB,此时点A对应的数是x,点B对应的数是1.因为AB=A′O,所以AB=|x﹣1|,因此,|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB.
探究求方程|x﹣1|=2的解
因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,﹣1.
探究:
求不等式|x﹣1|<2的解集
因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围.
请在图②的数轴上表示|x﹣1|<2的解集,并写出这个解集.
 (2)、探究二:探究 的几何意义
(2)、探究二:探究 的几何意义探究:
的几何意义
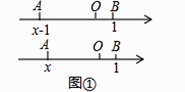
如图③,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),OP=|x|,OQ=|y|,在Rt△OPM中,PM=OQ=|y|,则MO= = = ,因此, 的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.
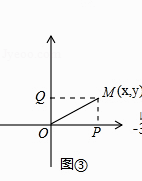
探究:
的几何意义
如图④,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究二(1)可知,A′O= ,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB= ,因此 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.
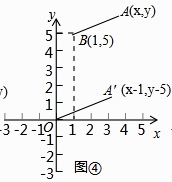
探究 的几何意义
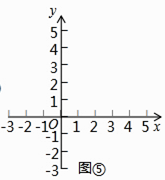
①请仿照探究二的方法,在图⑤中画出图形,并写出探究过程.
② 的几何意义可以理解为:
 (3)、拓展应用:
(3)、拓展应用:① + 的几何意义可以理解为:点A(x,y)与点E(2,﹣1)的距离和点A(x,y)与点F(填写坐标)的距离之和.
② + 的最小值为(直接写出结果)