2023年普通高等学校招生全国统一考试（全国II卷）

试卷更新日期：2023-01-16 类型：高考模拟

进入出卷网下载

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一个选项是符合题目要求的

1. 已知集合 $A = {x | x^{2} - 5 x + 6 \leq 0}$ ，集合 $B = {x | y = \sqrt{l o g_{2} (x - 1)}}$ ，则 $A \cup B =$ （）

A、 $(1 ， 3]$ B、 $(1 ， + \infty)$ C、 $[2 ， + \infty)$ D、 $[2 ， 3]$

查看试题解析
2. 设 $(a + 2 i) i = b + 3 i (a ， b \in R)$ ，则（）

A、 $a = 3$ ， $b = 2$ B、 $a = - 3$ ， $b = 2$ C、 $a = 3$ ， $b = - 2$ D、 $a = - 3$ ， $b = - 2$

查看试题解析
3. 已知向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = | \vec{b} | = | \vec{a} + \vec{b} |$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{5 π}{6}$ D、 $\frac{2 π}{3}$

查看试题解析
4. 我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，它体现了一种无限与有限的转化过程．比如在 $1 + \frac{1}{1 + \frac{1}{1 + \cdot \cdot \cdot}}$ 表达式中“…”既代表无限次重复，但原式却又是个定值，它可以通过方程 $1 + \frac{1}{x} = x$ 解得 $x = \frac{\sqrt{5} + 1}{2}$ ，类比上述方法，则 $\sqrt{2 + \sqrt{2 + \sqrt{\cdot \cdot \cdot}}} =$ （）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
5. 过抛物线 $y^{2} = 4 x$ 的焦点F的一条直线与此抛物线相交于A，B两点，已知 $A (4 ， 4)$ ，则线段 $A B$ 的中点到抛物线准线的距离是（）．

A、 $\frac{25}{8}$ B、 $\frac{25}{4}$ C、3 D、 $\frac{10}{3}$

查看试题解析
6. 若正整数N除以正整数m后的余数为n，则记为 $N \equiv n (m o d m)$ ，如 $10 \equiv 2 (m o d 4)$ .如图所示的程序框图的算法源于我国古代闻名中外的“中国剩余定理”.执行该程序框图，则输出的i等于（）

A、7 B、10 C、13 D、16

查看试题解析
7. 已知菱形ABCD的边长为2， $∠ B A D = 60 °$ ， E是AD的中点，沿BE将 $△ A B E$ 折起至 $△ P B E$ 的位置，使 $P D = \sqrt{2}$ ，则下列结论中错误的是（）．

A、平面 $P B E ⊥$ 平面PDE B、平面 $P B E ⊥$ 平面PBC C、平面 $P B E ⊥$ 平面BCDE D、平面 $P B D ⊥$ 平面BCDE

查看试题解析
8. 《九章算术》中有如下问题：今有蒲生一日，长四尺，莞生一日，长一尺．蒲生日自半，莞生日自倍．意思是：今有蒲第一天长高四尺，莞第一天长高一尺，以后蒲每天长高前一天的一半，莞每天长高前一天的两倍．请问第几天，莞的长度是蒲的长度的2倍（）

A、4天 B、5天 C、6天 D、7天

查看试题解析
9. 已知一个装满水的圆台形容器的上底半径为6，下底半径为1，高为 $5 \sqrt{3}$ ，若将一个铁球放入该容器中，使得铁球完全没入水中，则可放入的铁球的体积的最大值为（）

A、 $4 \sqrt{3} π$ B、 $32 \sqrt{3} π$ C、 $\frac{125 \sqrt{3} π}{2}$ D、 $108 π$

查看试题解析
10. 小陈准备将新买的《尚书·礼记》、《左传》、《孟子》、《论语》、《诗经》五本书立起来放在书架上，若要求《论语》、《诗经》两本书相邻，且《尚书·礼记》放在两端，则不同的摆放方法有（）

A、18种 B、24种 C、36种 D、48种

查看试题解析
11. 已知 $F$ 为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点，直线 $l$ 过点 $F$ 与双曲线交于 $A ， B$ 两点，且 $| A B |$ 最小值为 $\frac{2 b^{2}}{a}$ ，则双曲线离心率取值范围为（）

A、 $(1 ， 2)$ B、 $(1 ， \sqrt{2})$ C、 $(1 ， 2]$ D、 $(1 ， \sqrt{2}]$

查看试题解析
12. 让·巴普蒂斯·约瑟夫·傅里叶，法国欧塞尔人，著名数学家、物理学家．他发现任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示，如定义在R上的偶函数 $f (x) = \frac{π^{2}}{3} + 4 \sum_{n = 1}^{+ \infty} \frac{{(- 1)}^{n}}{n^{2}} c o s n x$ 满足 $f (2 π - x) = f (x)$ ，且当 $x \in [0 ， π]$ 时，有 $f (x) = x^{2}$ ，已知函数 $g (x) = f (x) - a (x + π)$ 有且仅有三个零点，则a的取值范围是（）

A、 $(- \frac{π}{2} ， - \frac{π}{4}) ∪ (\frac{π}{4} ， \frac{π}{2})$ B、 $(- \frac{π}{4} ， \frac{π}{4})$ C、 $(- \frac{π}{3} ， - \frac{π}{6}) ∪ (\frac{π}{6} ， \frac{π}{3})$ D、 $(- \frac{π}{6} ， \frac{π}{6})$

查看试题解析

二、填空题：本题共4小题，每小题5分，共20分

13. 自从申办冬奥成功之后，中国大力推广冰雪运动.统计数据显示，现中国从北到南总共有654块标准冰场和803块滑雪场，全国冰雪运动参与人数已达3.46亿人.一对酷爱冰雪运动的年轻夫妇，让刚好十个月大的孩子把“0､2､2､2､北､京”六张卡片排成一行，若依次排成“2022北京”或“北京2022”，就说“很好”，那么“很好”的概率是.

查看试题解析
14. 将函数 $f (x) = t a n 2 x$ 的图像向左平移 $t$ （ $t > 0$ ）个单位长度，得到函数g(x)的图像，若 $g (\frac{π}{2}) = 1$ ，则 $t$ 的最小值是．

查看试题解析
15. 设正实数 $a ， b$ 满足 $\frac{b}{a} + \frac{1}{b} = 1$ ，则 $a + 2 b$ 的最小值为．

查看试题解析
16. 已知双曲线 $C ： \frac{y^{2}}{4} - \frac{x^{2}}{b^{2}} = 1 (b > 0)$ 的上顶点、下焦点分别为M，F，以M为圆心，b为半径的圆与C的一条渐近线交于A，B两点，若 $∠ A M B = 60 °$ ， AB的中点为Q（Q在第一象限），点P在双曲线的下支上，则当 $| P F | + | P Q |$ 取得最小值时，直线PQ的斜率为．

查看试题解析

三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生按照要求作答。

17. 在 $Δ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ， $B = \frac{π}{4}$ ， $c = 3 \sqrt{2}$ ， $Δ A B C$ 的面积为 $6$ ．

(1)、求 $a$ 及 $s i n A$ 的值；

(2)、求 $s i n (2 A - \frac{π}{6})$ 的值．

查看试题解析
18. 如图，多面体 $A B C D E F$ 中， $A B C D$ 是菱形， $∠ A B C = 60 °$ ， $F A ⊥$ 平面 $A B C D$ ， $E D ∥ F A$ ，且 $A B = F A = 2 E D = 2$

(1)、求证：平面 $B D E ⊥$ 平面 $F A C$ ；

(2)、求二面角 $B - F C - E$ 的正弦值.

查看试题解析
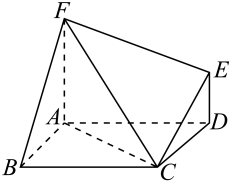19. 据悉强基计划的校考由试点高校自主命题，校考过程中达到笔试优秀才能进入面试环节．已知甲、乙两所大学的笔试环节都设有三门考试科目且每门科目是否达到优秀相互独立．若某考生报考甲大学，每门科目达到优秀的概率均为 $\frac{1}{3}$ ，若该考生报考乙大学，每门科目达到优秀的概率依次为 $\frac{1}{6}$ ， $\frac{2}{5}$ ， $n$ ，其中 $0 < n < 1$ ．

(1)、若 $n = \frac{1}{3}$ ，分别求出该考生报考甲、乙两所大学在笔试环节恰好有一门科目达到优秀的概率；

(2)、强基计划规定每名考生只能报考一所试点高校，若以笔试过程中达到优秀科目个数的期望为依据作出决策，该考生更希望进入甲大学的面试环节，求 $n$ 的范围．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）经过 $A (\frac{3}{2} ， \frac{1}{2})$ ， $B (\frac{3}{2} ， - \frac{1}{2})$ ， $D (- \frac{3}{2} ， \frac{\sqrt{2}}{2})$ ， $E (0 ， 1)$ ， $G (- 1 ， 0)$ 五个点中的三个．

(1)、求椭圆C的方程．

(2)、直线l与椭圆C交于P，Q两点，且与圆O： $x^{2} + y^{2} = \frac{3}{4}$ 相切，证明： $△ P O Q$ 为直角三角形．

查看试题解析
21. 已知函数 $f (x) = \frac{l n x + a}{x + 1}$ .

(1)、若 $f^{'} (1) = \frac{1}{4}$ ，求 $a$ 的值；

(2)、当 $a > 2$ 时，
①求证： $f (x)$ 有唯一的极值点 $x_{1}$ ；
②记 $f (x)$ 的零点为 $x_{0}$ ，是否存在 $a$ 使得 $\frac{x_{1}}{x_{0}} \leq e^{2}$ ？说明理由.

查看试题解析

四、选修4-4：坐标系与参数方程

22. 在直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = \sqrt{3} + t \\ y = - 2 + \sqrt{3} t \end{array}$ （ $t$ 为参数），以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ s i n^{2} θ = 4 c o s θ$ .

(1)、求直线 $l$ 的普通方程与曲线 $C$ 的直角坐标方程；

(2)、已知点 $P$ 的直角坐标为 $(2 ， 0)$ ，过点 $P$ 作直线 $l$ 的垂线交曲线 $C$ 于 $D$ 、 $E$ 两点（ $D$ 在 $x$ 轴上方），求 $\frac{1}{| P D |} - \frac{1}{| P E |}$ 的值.

查看试题解析

五、选修4-5：不等式选讲

23. 设a，b，c均为正数，且 $a + b + c = 1$ ．

(1)、求 $\frac{1}{a} + \frac{4}{b + c}$ 的最小值；

(2)、证明： $\sqrt{1 - a} + \sqrt{1 - b} + \sqrt{1 - c} ≤ \sqrt{6}$ ．

查看试题解析