2022-2023初中数学浙教版七上期末模拟试卷
试卷更新日期:2023-01-15 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 下列说法正确的是( )
①有理数包括正有理数和负有理数 ②相反数大于本身的数是负数
③数轴上原点两侧的数互为相反数 ④两个数比较,绝对值大的反而小
A、② B、①③ C、①② D、②③④2. 下列结论中,正确的是( )A、单项式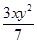 的系数是3,次数是2.
B、单项式m的次数是1,没有系数.
C、单项式﹣xy2z的系数是﹣1,次数是4.
D、多项式5x2-xy+3是三次三项式.
3. 若∠AOB=90°,∠BOC=40°,则∠AOC的度数为( )A、50° B、50° 或120° C、50°或130° D、130°4. 若a是有理数,那么在①a+1,②|a+1|,③|a|+1,④a2+1中,一定是正数的有( )A、1个 B、2个 C、3个 D、4个5. 如果ab≠0,那么的值不可能是( )A、0 B、1 C、2 D、-26. 若方程:2(x-1)-6=0与的解互为相反数,则a的值为( )A、 B、 C、 D、-17. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm8. 有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个
的系数是3,次数是2.
B、单项式m的次数是1,没有系数.
C、单项式﹣xy2z的系数是﹣1,次数是4.
D、多项式5x2-xy+3是三次三项式.
3. 若∠AOB=90°,∠BOC=40°,则∠AOC的度数为( )A、50° B、50° 或120° C、50°或130° D、130°4. 若a是有理数,那么在①a+1,②|a+1|,③|a|+1,④a2+1中,一定是正数的有( )A、1个 B、2个 C、3个 D、4个5. 如果ab≠0,那么的值不可能是( )A、0 B、1 C、2 D、-26. 若方程:2(x-1)-6=0与的解互为相反数,则a的值为( )A、 B、 C、 D、-17. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm8. 有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个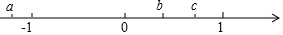 A、4 B、3 C、2 D、19. 如图,已知A,O,B在一条直线上,∠1是锐角,则∠1的余角是( )
A、4 B、3 C、2 D、19. 如图,已知A,O,B在一条直线上,∠1是锐角,则∠1的余角是( )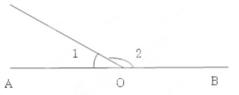 A、 B、 C、 D、∠2-∠110.
A、 B、 C、 D、∠2-∠110.如图所示,则图中三角形的个数一共是( )
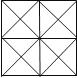 A、16 B、32 C、40 D、44
A、16 B、32 C、40 D、44二、填空题(每空2分,共18分)
-
11. 某冬天中午的温度是5℃,下午上升到7℃,由于冷空气南下,到夜间又下降了9℃,则这天夜间的温度是℃.
12. ∠1还可以用表示,若∠1=62.16°,那么62.16°=°′″.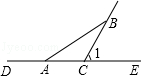 13. 明买了20本练习本,店主给他八折优惠,结果便宜1.6元,每本练习本的标价是元 。14. 如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么 .
13. 明买了20本练习本,店主给他八折优惠,结果便宜1.6元,每本练习本的标价是元 。14. 如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么 . 15. ;16.
15. ;16.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a﹣b|.
所以式子|x﹣2|的几何意义是数轴上表示x的点与表示2的点之间的距离.借助于数轴回答下列问题:
①数轴上表示2和5两点之间的距离是 , 数轴上表示1和﹣3的两点之间的距离是 .
②数轴上表示x和﹣2的两点之间的距离表示为 .
③数轴上表示x的点到表示1的点的距离与它到表示﹣3的点的距离之和可表示为:|x﹣1|+|x+3|.则|x﹣1|+|x+3|的最小值是 .
④若|x﹣3|+|x+1|=8,则x=
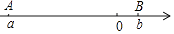
三、解答题(共8题,共52分)
-
17. 计算题:(1)、(2)、18. 解方程:(1)、6-3x=2(2-x);(2)、-1=.19. 先化简再求值: , 其中a=-1,b=2.20. 在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天航行路程记录如下:14,﹣9,﹣18,﹣7,13,﹣6,10,﹣5(单位:千米).
(1)B地在A地何位置?
(2)若冲锋舟每千米耗油0.5升,出发前冲锋舟油箱有油29升,求途中需补充多少升油?
21. 一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元,求每件服装的标价是多少元?22. 如图,∠AOC与∠BOC的度数比为5:2,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.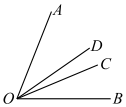 23. 安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案:
23. 安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案:方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
24. 【定义】:在同一直线上的三点A、B、C,若满足点C到另两个点A、B的距离具有2倍关系,则我们就称点C是其余两点的强点 或弱点 具体地:①当点C在线段AB上时,若 ,则称点C是【A,B】的强点;若 ,则称点C是【B,A】的强点;
②当点C在线段AB的延长线上时,若 ,则称点C是【A,B】的弱点;
【例如】如图,数轴上点A、B、C、D分别表示数 、2、1、0,则点C是【A,B】的强点,又是【A,D】的弱点;点D是【B,A】的强点,又是【B,C】的弱点;
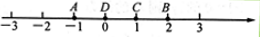
【应用】Ⅰ.如图,M、N为数轴上两点,点M所表示的数为 ,点N所表示的数为4.
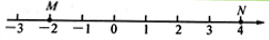
【M,N】的强点表示的数为 .
【N,M】的弱点表示的数为 .
Ⅱ.如图,数轴上,点A所表示的数为 ,点B所表示的数为 一只电子蚂蚁P从点B出发,以4个单位每秒的速度沿数轴向左运动,设运动时间为t秒

求当t为何值时?P是【B,A】的弱点.
求当t为何值时?P、A、B三个点中恰有一个点为其余两点的强点.