2022-2023学年初数北师大版八年级下册1. 2 直角三角形 同步必刷题
试卷更新日期:2023-01-14 类型:同步测试
一、单选题
-
1. 下列三角形中,不是直角三角形的是( )A、中, B、中, , C、中, D、中,三边之比为2. 如图,在中, , 是高,能直接判断的依据是( )
 A、 B、 C、 D、3. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( )
A、 B、 C、 D、3. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( ) A、AC=DF,BC=EF B、∠A=∠D,AB=DE C、AC=DF,AB=DE D、∠B=∠E,BC=EF4. 如图,在△ABC中, , D是上一点,于点E, , 连接 , 若 , 则等于( )
A、AC=DF,BC=EF B、∠A=∠D,AB=DE C、AC=DF,AB=DE D、∠B=∠E,BC=EF4. 如图,在△ABC中, , D是上一点,于点E, , 连接 , 若 , 则等于( ) A、6 B、7 C、8 D、95. 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A、6 B、7 C、8 D、95. 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( ) A、60° B、75° C、90° D、120°6. 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A、60° B、75° C、90° D、120°6. 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )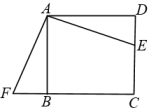 A、4 B、8 C、16 D、无法计算7. 下列命题:①成轴对称的两个三角形是全等三角形;②当a>b时,若c>0,则ac>bc;③直角三角形中斜边上的中线等于斜边的一半;④内错角相等,其中原命题与逆命题均为真命题的个数是( )A、1个 B、2个 C、3个 D、4个8. 如图,是直角三角形,点C在数轴上对应的数为 , 目 , , 若以点C为圆心,为半径画弧交数轴于点M,则A,M两点间的距离为( )
A、4 B、8 C、16 D、无法计算7. 下列命题:①成轴对称的两个三角形是全等三角形;②当a>b时,若c>0,则ac>bc;③直角三角形中斜边上的中线等于斜边的一半;④内错角相等,其中原命题与逆命题均为真命题的个数是( )A、1个 B、2个 C、3个 D、4个8. 如图,是直角三角形,点C在数轴上对应的数为 , 目 , , 若以点C为圆心,为半径画弧交数轴于点M,则A,M两点间的距离为( ) A、0.4 B、 C、 D、9. 在北京召开的国际数学家大会会标,它是有四个全等的直角三角形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形的面积是1,较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
A、0.4 B、 C、 D、9. 在北京召开的国际数学家大会会标,它是有四个全等的直角三角形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形的面积是1,较长的直角边为a,较短的直角边为b,则(a+b)2的值为( ) A、13 B、19 C、25 D、16910. 如图,已知长方形纸片ABCD,点E在边AB上,且BE=2,BC=3,将△CBE沿直线CE翻折,使点B落在点G,延长EG交CD于点F处,则线段FG的长为( )
A、13 B、19 C、25 D、16910. 如图,已知长方形纸片ABCD,点E在边AB上,且BE=2,BC=3,将△CBE沿直线CE翻折,使点B落在点G,延长EG交CD于点F处,则线段FG的长为( ) A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题
-
11. 已知直角三角形两直角边长分别为3和5,则斜边长为 .12. 如图,三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母M所代表的正方形面积是.
 13. 如图,梯形ABCD中,∠ABC=∠BCD,AD∥BC,BD平分∠ABC,若AD=3,BC=7,则BD的长为 .
13. 如图,梯形ABCD中,∠ABC=∠BCD,AD∥BC,BD平分∠ABC,若AD=3,BC=7,则BD的长为 . 14. 如图,点D在内, , , , , 则图中阴影部分的面积为 .
14. 如图,点D在内, , , , , 则图中阴影部分的面积为 . 15. 如图,中, , , , 是的中点,是上一动点,则的最小值为.
15. 如图,中, , , , 是的中点,是上一动点,则的最小值为. 16. 如图,有一张直角三角形纸片,两直角边AC=4cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长是 .
16. 如图,有一张直角三角形纸片,两直角边AC=4cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长是 . 17. 已知a、b、c是一个三角形的三边长,如果满足 , 则这个三角形的形状是 .18. 如图,在中, , 且是边上的中线,于若 , , 则的长为.
17. 已知a、b、c是一个三角形的三边长,如果满足 , 则这个三角形的形状是 .18. 如图,在中, , 且是边上的中线,于若 , , 则的长为. 19. 在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,∠BAC=90°,在△ABC的面积是.
19. 在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,∠BAC=90°,在△ABC的面积是. 20. 如图,已知点是长方形中边上一点,将四边形沿直线折叠,折叠后点的对应点为 , 点的对应点为 , 若点在上,且 , , 则 .
20. 如图,已知点是长方形中边上一点,将四边形沿直线折叠,折叠后点的对应点为 , 点的对应点为 , 若点在上,且 , , 则 .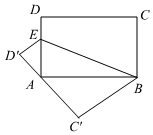
三、解答题
-
21. 如图,正方形网格中的每个小方格边长均为1,的顶点在格点上,判断的形状,并说明理由.
 22. 如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
22. 如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积. 23. 如图,在中,是上一点,若 , , , .
23. 如图,在中,是上一点,若 , , , .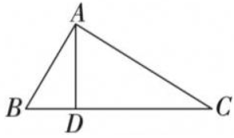 (1)、求证:;(2)、求的面积.
(1)、求证:;(2)、求的面积.


