人教版八年级数学2023年寒假专项训练----复习部分第十四章整式的乘法与因式分解 B卷

试卷更新日期：2023-01-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列因式分解正确的是（）

A、x²-x＝x（x+1） B、a²-3a-4＝（a+4）（a-1） C、a²+2ab-b²＝（a-b）² D、x²-y²＝（x+y）（x-y）

查看试题解析
2. 下列多项式乘以多项式中，能用平方差公式计算的是（）

A、 $(- x - y) (- x + y)$ B、 $(x - y) (- x + y)$ C、 $(- x - y) (x + y)$ D、 $(- x - y) (- x - y)$

查看试题解析
3. 下列因式分解正确的是（）

A、 $x^{2} + 4 = (x - 2) (x + 2)$ B、 $x^{2} - 2 x + 1 = {(x - 1)}^{2}$ C、 $x^{2} - x = x^{2} (1 - \frac{1}{x})$ D、 $x^{4} - 1 = (x^{2} + 1) (x^{2} - 1)$

查看试题解析
4. 多项式 $12 m^{3} n^{2} + 8 m^{2} n - 20 m^{2} n^{3}$ 的公因式是（）

A、 $4 m^{2} n$ B、 $4 m^{2} n^{2}$ C、 $2 m n$ D、 $8 m^{2} n$

查看试题解析
5. 计算 ${(\frac{2}{3})}^{2020} \times {(\frac{3}{2})}^{2021}$ 的结果是（）

A、 $\frac{2}{3}$ B、 $- \frac{2}{3}$ C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

查看试题解析
6. （2+1）（2²+1）（2⁴+1）…（2¹⁶+1）的结果为（）

A、2³²-1 B、2³²+1 C、2³² D、2¹⁶

查看试题解析
7. 若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为40；其中5个如图2摆放，构造出一个长方形，其中阴影部分面积为100（各个小长方形之间不重叠不留空），则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析

二、填空题

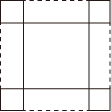
8. 在实数范围内分解因式： $x^{2} - 3 x - 1 =$ .

查看试题解析
9. 计算 ${(- 2 y^{3})}^{3}$ 的结果等于．

查看试题解析
10. 若 $(x + 3) (x + m) = x^{2} - 2 x - 15$ ．则m＝．

查看试题解析
11. 若素数p，使得 $4 p^{2} + p + 81$ 是一个完全平方数，则p=.（若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数.）

查看试题解析
12. $m > 0$ ， $n > 0$ ，若 $m^{2} + 4 n^{2} = 13$ ， $m n = 3$ ，请借助下图直观分析，通过计算求得 $m + 2 n$ 的值为．

查看试题解析

三、解答题

13. 仔细阅读下面例题，解答问题：
例题：已知二次三项式 $x^{2} - 4 x + m$ 有一个因式是 $x + 3$ ，求另一个因式以及m的值．
解：设另一个因式为 $x + n$ ，则 $x^{2} - 4 x + m = (x + 3) (x + n)$ ，
即 $x^{2} - 4 x + m = x^{2} + (n + 3) x + 3 n$ ，
∴ ${\begin{array}{l} n + 3 = - 4 \\ 3 n = m \end{array}$ ，解得 ${\begin{array}{l} m = - 21 \\ n = - 7 \end{array}$ ．
故另一个因式为 $x - 7$ ， m的值为－21．
仿照上面的方法解答下面问题：
已知二次三项式 $x^{2} + 3 x - k$ 有一个因式是x-5，求另一个因式以及k的值．

查看试题解析

四、综合题

14. 阅读材料后解决问题：
小明遇到下面一个问题：
计算（2+1）（2²+1）（2⁴+1）（2⁸+1）．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：（2+1）（2²+1）（2⁴+1）（2⁸+1）
=（2+1）（2﹣1）（2²+1）（2⁴+1）（2⁸+1）
=（2²﹣1）（2²+1）（2⁴+1）（2⁸+1）
=（2⁴﹣1）（2⁴+1）（2⁸+1）
=（2⁸﹣1）（2⁸+1）
=2¹⁶﹣1
请你根据小明解决问题的方法，试着解决以下的问题：

(1)、（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）= ．

(2)、（3+1）（3²+1）（3⁴+1）（3⁸+1）（3¹⁶+1）= ．

(3)、化简：（m+n）（m²+n²）（m⁴+n⁴）（m⁸+n⁸）（m¹⁶+n¹⁶）．

查看试题解析
15. 某校数学社团的小亮、小颖两个同学利用分组分解法进行的因式分解：
小亮： $m^{2} - m n + 2 m - 2 n$
= $(m^{2} - m n) + (2 m - 2 n)$
= $m (m - n) + 2 (m - n)$
= $(m - n) (m + 2)$
小颖： $4 x^{2} - y^{2} - z^{2} + 2 y z$
$= 4 x^{2} - (y^{2} + z^{2} - 2 y z)$
= $2 x^{2} - (y - z)^{2}$
$= (2 x + y - z) (2 x - y + z)$ ．
请你在他们解法的启发下，解决下面问题；

(1)、因式分解 $a^{3} - 3 a^{2} - 9 a + 27$ ；

(2)、因式分解 $x^{2} - 4 x y + 4 y^{2} - 16$ ；

(3)、已知a，b，c是 $Δ A B C$ 的三边，且满足 $a^{2} - a b + c^{2} = 2 a c - b c$ ，判断 $Δ A B C$ 的形状并说明理由．

查看试题解析

人教版八年级数学2023年寒假专项训练----复习部分 第十四章 整式的乘法与因式分解 B卷

一、单选题

二、填空题

三、解答题

四、综合题

人教版八年级数学2023年寒假专项训练----复习部分第十四章整式的乘法与因式分解 B卷