人教版八年级数学2023年寒假专项训练----复习部分 第十二章 全等三角形 B卷
试卷更新日期:2023-01-14 类型:复习试卷
一、单选题
-
1. 下列各组图形中,是全等形的是( )A、两个含30°角的直角三角形 B、一个钝角相等的两个等腰三角形 C、边长为5和6的两个等腰三角形 D、腰对应相等的两个等腰直角三角形2. (1)两边和一角对应相等的两个三角形全等;(2)三个内角对应相等的两个三角形全等;(3)斜边对应相等的两个等腰直角三角形全等;(4)两边和第三边上的高对应相等的两个三角形全等.其中正确的个数为( )A、1 B、2 C、3 D、43. 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
 A、2 B、4 C、4.5 D、34. 如图, , , , 则的度数是( )
A、2 B、4 C、4.5 D、34. 如图, , , , 则的度数是( ) A、22° B、23° C、30° D、33°5. 如图,已知方格纸中是4个相同的正方形,则( )
A、22° B、23° C、30° D、33°5. 如图,已知方格纸中是4个相同的正方形,则( )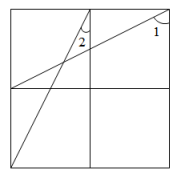 A、60° B、90° C、120° D、150°6. 如图,点B,E,C,F在同一直线上,△ABC≌△DEF,BC=8,BF=13,则BE的长为( )
A、60° B、90° C、120° D、150°6. 如图,点B,E,C,F在同一直线上,△ABC≌△DEF,BC=8,BF=13,则BE的长为( ) A、4 B、5 C、6.5 D、87. 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A、4 B、5 C、6.5 D、87. 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )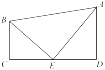 A、BC+AD=CD B、E为CD中点 C、∠AEB=90° D、S△ABE=S四边形ABCD8. 如图,在和中, . 连接AC,BD交于点M,连接OM.则下列结论:①;②;③平分;④平分 . 其中正确结论的个数为( )
A、BC+AD=CD B、E为CD中点 C、∠AEB=90° D、S△ABE=S四边形ABCD8. 如图,在和中, . 连接AC,BD交于点M,连接OM.则下列结论:①;②;③平分;④平分 . 其中正确结论的个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. 如图,在中, , 以点A为圆心,任意长为半径作弧,分别交边、于点M、N,分别以点M、N为圆心,以大于为半径作弧,两弧交于点P,射线交于点D,若 , 则的面积为 .
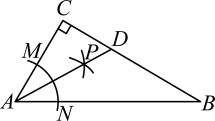 10. 如图, , 且 , 于E,于F.若 , , , 则的长为.
10. 如图, , 且 , 于E,于F.若 , , , 则的长为. 11. 如图,在中, , 平分交于点 , 垂足为E.若 , , 则的长为.
11. 如图,在中, , 平分交于点 , 垂足为E.若 , , 则的长为. 12. 如图,在长方形ABCD中, , , 延长BC到点E,使 , 连接DE,动点P从点B出发,以每秒2个单位的速度沿BC—CD—DA向终点A运动,设点P的运动时间为t(秒),当和全等时,t的值为 .
12. 如图,在长方形ABCD中, , , 延长BC到点E,使 , 连接DE,动点P从点B出发,以每秒2个单位的速度沿BC—CD—DA向终点A运动,设点P的运动时间为t(秒),当和全等时,t的值为 . 13. 如图,在四边形ABCD中,E为边AD上一点, , 且 , , , , 则AB的长度为 .
13. 如图,在四边形ABCD中,E为边AD上一点, , 且 , , , , 则AB的长度为 .
三、解答题
-
14. 已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
 15. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
15. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD 16. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
16. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .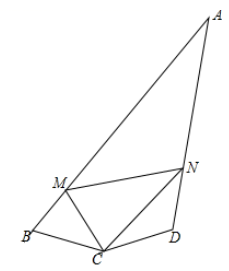
四、综合题
-
17. 如图,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD、CE交于点F,CD=CG,连结FG.
 (1)、求证:FD=FG;(2)、线段FG与FE之间有怎样的数量关系,请说明理由;(3)、若∠B≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.18. 如图
(1)、求证:FD=FG;(2)、线段FG与FE之间有怎样的数量关系,请说明理由;(3)、若∠B≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.18. 如图 (1)、如图①,在四边形中, , , , 分别是边 , 上的点,且 . 请直接写出线段 , , 之间的数量关系:;(2)、如图②,在四边形中, , , , 分别是边 , 上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , , 分别是边 , 所在直线上的点,且 . 请画出图形(除图②外),并直接写出线段 , , 之间的数量关系.
(1)、如图①,在四边形中, , , , 分别是边 , 上的点,且 . 请直接写出线段 , , 之间的数量关系:;(2)、如图②,在四边形中, , , , 分别是边 , 上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , , 分别是边 , 所在直线上的点,且 . 请画出图形(除图②外),并直接写出线段 , , 之间的数量关系.