2022-2023学年初数北师大版八年级下册 2.5 一元一次不等式与一次函数 同步必刷题
试卷更新日期:2023-01-14 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,直线过点A、B,则不等式的解集是( )
 A、 B、 C、 D、2. 如图,直线经过点 , 则关于x的不等式解集为( )
A、 B、 C、 D、2. 如图,直线经过点 , 则关于x的不等式解集为( )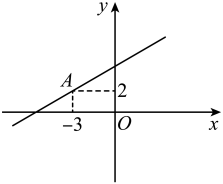 A、 B、 C、 D、3. 如图,直线经过点A和点B,直线过点A,则不等式的解集为( )
A、 B、 C、 D、3. 如图,直线经过点A和点B,直线过点A,则不等式的解集为( ) A、 B、 C、 D、4. 如图,一次函数与一次函数的图象交于点 , 则关于x的不等式的解集是( )
A、 B、 C、 D、4. 如图,一次函数与一次函数的图象交于点 , 则关于x的不等式的解集是( ) A、 B、 C、 D、5. 一次函数y=kx+b的图象如图所示,当kx+b>3时,x的取值范围是( )
A、 B、 C、 D、5. 一次函数y=kx+b的图象如图所示,当kx+b>3时,x的取值范围是( )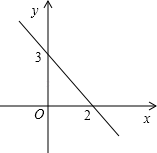 A、x>0 B、x<0 C、x<2 D、x>26. 如图,直线与()的交点的横坐标为 , 则关于x的不等式的解集为( )
A、x>0 B、x<0 C、x<2 D、x>26. 如图,直线与()的交点的横坐标为 , 则关于x的不等式的解集为( )
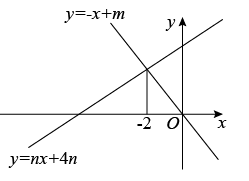 A、 B、 C、 D、7. 如图,在同一平面直角坐标系中,一次函数的图象与正比例函数的图象相交于点A,且点A的纵坐标是2,则不等式的解集是( )
A、 B、 C、 D、7. 如图,在同一平面直角坐标系中,一次函数的图象与正比例函数的图象相交于点A,且点A的纵坐标是2,则不等式的解集是( )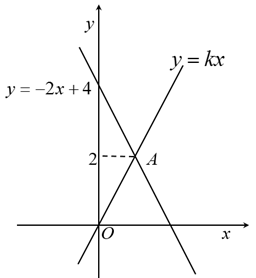 A、 B、 C、 D、8. 我们知道,若ab>0.则有或 . 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A、 B、 C、 D、8. 我们知道,若ab>0.则有或 . 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( ) A、x>2 B、-0.5<x<2 C、0<x<2 D、x<-0.5或x>29. 若方程2x=4的解使关于x的一次不等式(a-1)x<a+5成立,则a的取值范围是( )A、a≠1 B、a>7 C、a<7 D、a<7且a≠110. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )
A、x>2 B、-0.5<x<2 C、0<x<2 D、x<-0.5或x>29. 若方程2x=4的解使关于x的一次不等式(a-1)x<a+5成立,则a的取值范围是( )A、a≠1 B、a>7 C、a<7 D、a<7且a≠110. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )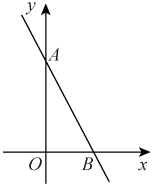 A、 B、x>3 C、 D、x<3
A、 B、x>3 C、 D、x<3二、填空题(每题3分,共30分)
-
11. 如图,一次函数的图象交x轴于点 , 则关于x的不等式的解集为 .
 12. 如图,直线:与直线:相交于点 , 则关于x的不等式的解集为 .
12. 如图,直线:与直线:相交于点 , 则关于x的不等式的解集为 . 13. 如图,一次函数的图象经过点(0,1)和(2,0),则不等式的解集是 .
13. 如图,一次函数的图象经过点(0,1)和(2,0),则不等式的解集是 . 14. 如图,直线分别交x轴、y轴于点A、C,直线分别交x轴、y轴于点B、D,直线AC与直线BD相交于点 , 则不等式的解集为 .
14. 如图,直线分别交x轴、y轴于点A、C,直线分别交x轴、y轴于点B、D,直线AC与直线BD相交于点 , 则不等式的解集为 . 15. 设一次函数 . 若当时,;当时, , 则b的取值范围是16. 如图,已知直线和直线的交点坐标是(m,n),则关于x的不等式的解集是 .
15. 设一次函数 . 若当时,;当时, , 则b的取值范围是16. 如图,已知直线和直线的交点坐标是(m,n),则关于x的不等式的解集是 . 17. 如图,直线与交于点 , 则关于的不等式的解集为 .
17. 如图,直线与交于点 , 则关于的不等式的解集为 . 18. 对于一次函数y=3x-2,当y>0时,自变量x的取值范围是 .19. 如果直线和直线的交点坐标为 , 则不等式的解集是 .20. 已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 .
18. 对于一次函数y=3x-2,当y>0时,自变量x的取值范围是 .19. 如果直线和直线的交点坐标为 , 则不等式的解集是 .20. 已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 .
三、解答题(共6题,共60分)
-
21. 当自变量x满足什么条件时,的函数值不小于的函数值?22. 如下图,一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2,1);
 (1)、求出m,k的值.(2)、若y1> y2 , 请直接写出x的取值范围.23. 已知一次函数的图像与轴的交点在轴的上方,且随 的增大而减小.(1)、求整数的值;(2)、在(1)的结论下,在下面的平面直角坐标系中画出函数的图象,并根据图像回答:当取何值时,? ? ?
(1)、求出m,k的值.(2)、若y1> y2 , 请直接写出x的取值范围.23. 已知一次函数的图像与轴的交点在轴的上方,且随 的增大而减小.(1)、求整数的值;(2)、在(1)的结论下,在下面的平面直角坐标系中画出函数的图象,并根据图像回答:当取何值时,? ? ? 24. 在平面直角坐标系中,一次函数的图象是由函数的图象平移得到,且经过点 .(1)、求这个一次函数的解析式;(2)、当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.25. 如图,在平面直角坐标系中,一次函数与轴交于 , 且与正比例函数图象交于点 .
24. 在平面直角坐标系中,一次函数的图象是由函数的图象平移得到,且经过点 .(1)、求这个一次函数的解析式;(2)、当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.25. 如图,在平面直角坐标系中,一次函数与轴交于 , 且与正比例函数图象交于点 . (1)、求一次函数的解析式;(2)、直接写出时,的取值范围.26. 我区应国家号召,认真贯彻落实党的二十大精神,全面推进乡村振兴,把富民政策一项一项落实好,特将农户种植的农产品包装成A、B两种大礼包.某超市预购进两种大礼包共400个,两种大礼包的进价和预售价如表.设购进A种大礼包x个,且所购进的两种大礼包能全部卖完时获得的总利润为W元.
(1)、求一次函数的解析式;(2)、直接写出时,的取值范围.26. 我区应国家号召,认真贯彻落实党的二十大精神,全面推进乡村振兴,把富民政策一项一项落实好,特将农户种植的农产品包装成A、B两种大礼包.某超市预购进两种大礼包共400个,两种大礼包的进价和预售价如表.设购进A种大礼包x个,且所购进的两种大礼包能全部卖完时获得的总利润为W元.大礼包类型
进价/(元/个)
售价/(元/个)
A
47
65
B
37
50
(1)、求W关于x的函数表达式(不要求写x的取值范围);(2)、如果购进两种大礼包的总费用不超过18000元,那么商场如何进货才能获得最大利润?最大利润是多少?