浙江省温州二中2022-2023学年九年级上学期第三次月考数学试卷

试卷更新日期：2023-01-14 类型：月考试卷

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分）

1. 已知⊙O的半径为8cm，点P在⊙O上，则OP的长为（）

A、2cm B、4cm C、8cm D、16cm

查看试题解析
2. 书架上有2本数学书、1本物理书．从中任取1本书是物理书的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 将抛物线y＝2x²向左平移3个单位，所得抛物线的解析式是（）

A、y＝2（x+3）² B、y＝2（x-3）² C、y＝2x²+3 D、y＝2x²-3

查看试题解析
4. 如图，∠α的顶点为O，一边在x轴的正半轴上，另一边上有一点P（3，4），则sinα＝（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

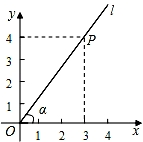查看试题解析
5. 如图，测量小玻璃管口径的量具ABC，AB的长为3cm，AC被分为6等份．若小玻璃管口DE正好对着量具上2等份处（DE∥AB），那么小玻璃管口径DE的长为（）

A、1cm B、 $\frac{9}{5}$ cm C、2cm D、 $\frac{12}{5}$ cm

查看试题解析
6. 如图，AB是⊙O的直径，弦CD⊥AB于点E，如果AB＝20，CD＝16，那么线段OE的长为（）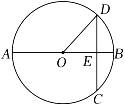

A、4 B、6 C、8 D、9

查看试题解析
7. 如图，正八边形ABCDEFGH中，∠EAG大小为（）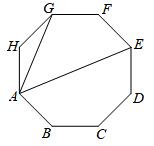

A、30° B、40° C、45° D、50°

查看试题解析
8. 已知抛物线y＝x²+2mx+2022（m为常数）上有三点，点A（-m-1，y₁），点B（-m+1.5，y₂），点C（2-m，y₃），则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＞y₂＞y₃ B、y₃＞y₁＞y₂ C、y₁＞y₃＞y₂ D、y₃＞y₂＞y₁

查看试题解析
9. 如图，在由边长为1的小正方形组成的网格中，点A，B，C，D都在格点上，点E在AB的延长线上，以A为圆心，AE为半径画弧，交AD的延长线于点F，且弧EF经过点C，则 $\overset{⌢}{E F}$ 的长为（）

A、 $\frac{\sqrt{5} π}{4}$ B、 $\frac{5 π}{4}$ C、 $\frac{\sqrt{5} π}{8}$ D、 $\frac{5 π}{8}$

查看试题解析
10. 如图，已知点C是线段AB的中点，CD⊥AB且CD＝ $\frac{1}{2}$ AB＝a，延长CB至E，使得BE＝b，以CD，CE为边作矩形CEFD，连接并延长DB，交FE的延长线于点G，连接AG，《几何原本》中利用该图解释了代数式（2a+b）²+b²＝2[（a+b）²+a²]的几何意义，以AG为直径作圆，交AF于点H，若a＝9，b＝6，则HG的长为（）

A、5 $\sqrt{13}$ B、18 C、3 $\sqrt{34}$ D、17

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

11. 已知线段a＝4厘米，c＝9厘米，那么线段a和c的比例中项是厘米．

查看试题解析
12. 抛物线y＝x²+2x-1的对称轴是．

查看试题解析
13. 小文将学校二维码打印在面积为400cm²的正方形纸上，如图所示，为了估计图中黑色部分的面积，她在纸内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的面积约为 cm² ．

查看试题解析
14. 如图，点D是△ABC的重心，延长AD交BC于点O，△DEF是由△ABC经过位似变化得到的，点O是位似中心，则△DEF与△ABC的面积比是．

查看试题解析
15. 如图，在半径为6，圆心角为90°的扇形OAB中， $\overset{⌢}{B C}$ ＝2 $\overset{⌢}{A C}$ ，点D是半径OB的中点，点P从点D出发，沿D→O→A的方向运动到A的过程中（包括D，A点），线段BP，CP与 $\overset{⌢}{B C}$ 所围成的区域（如图中阴影部分）面积的最小值为．

查看试题解析
16. 图1是某个零件横截面的示意图，已知AB＝CD，∠B＝∠C，为了求出BC的长度，小艺将一根直尺按图2，图3，图4的三种方式摆放，所测得的具体数据（单位：cm）如图所示，则直尺宽为 cm，BC为 cm．

查看试题解析

三、解答题（本题有8小题，共80分）

17. 计算：

(1)、已知 $\frac{y}{2} = \frac{2 y - x}{3}$ ，求 $\frac{x}{y}$ 的值．

(2)、tan60°+cos²45°-sin²30°．

查看试题解析
18. 一个布袋中有8个红球和16个白球，它们除颜色外都相同．

(1)、求从袋中摸出一个球是红球的概率；

(2)、现从袋中取走若干个白球，并放入相同数量的红球．搅拌均匀后，要使从袋中摸出一个球是红球的概率是 $\frac{5}{8}$ ，问取走了多少个白球？（要求通过列式或列方程解答）

查看试题解析
19. 在Rt△ABC中，∠C＝90°，BC＝2，sinA＝ $\frac{1}{3}$ ，求AC，AB及sinB的值．

查看试题解析
20. 如图，在6×6的方格中，有一格点△ABC（顶点都在小正方形的顶点上）及格点P，按下列要求画格点三角形．

(1)、在图1中，画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C'．

(2)、在图2中，画出△ABC绕某一点顺时针旋转90°后的△DEF，且点P在△DEF内（不包括边界）．

查看试题解析
21. 如图，顶点为M的抛物线y＝a（x- $\frac{3}{2}$ ）²-1经过原点O，与x轴正半轴交于点A，对称轴交x轴于点N．

(1)、求a的值．

(2)、B是第二象限抛物线上一点，BE∥x轴，交y轴于点C，交对称轴于点D，交抛物线于点E．连结BM交x轴于点F，交y轴于点G．若MF＝FG，求CD：DE的值．

查看试题解析
22. 四边形ABCD内接于⊙O，C为 $\overset{⌢}{B D}$ 的中点，OC交BD于点M，DG⊥AB于点G．已知CM＝2，OM＝3．

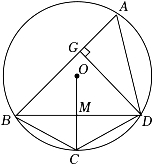(1)、求弦BD的长．

(2)、若sin∠ABD＝ $\frac{3}{4}$ ，求四边形ABCD的面积．

查看试题解析

23. 根据以下素材，探索完成任务．

如何设计喷灌器喷水口的升降方案
素材1	随着自动化设备的普及，家庭庭院也引入自动喷灌系统．图1中某庭院内有一个可垂直升降的草坪喷灌器，从喷水口喷出的水柱成抛物线形．图2是该喷灌器OA喷水时的截面示意图，喷水口A点离地高度为0.25m，喷出的水柱在离喷水口水平距离为2m处达到最高，高度为0.45m，且水柱刚好落在庭院围墙和地面的交界B点处．
素材2	为了美化庭院，准备在庭院内沿围墙建花坛种植绣球花，花坛高0.4m，宽0.8m，侧面用大理石包围，长方形BCDE是花坛截面，如图3．调整喷水口的高度，喷出的水柱形状与原来相同，水柱落在花坛的上方DE边上（大理石厚度不计），达到给花坛喷灌的效果．
问题解决
任务1	确定水柱的形状	在图2中，建立合适的平面直角坐标系，求抛物线的表达式．
任务2	确定喷灌器的位置	求出喷灌器OA与围墙的距．
任务3	拟定喷头升降方案	调整喷水口的高度，使水柱可以喷灌花坛，求喷水口距离地面高度的最小值．

查看试题解析

24. 如图，矩形ABCD中，AB＝4，BC＝8．点E从点A出发沿AD向终点D运动，同时点F从点C出发沿CB向终点B运动，满足AE＝CF＝a，点D'与点D关于直线EF对称，DD'交直线CB于点G．

(1)、当点D'与点A重合时，求EF的长；

(2)、若点G在线段BC上；
①请直接给出a的取值范围 ▲ ；

②当BG＝FC时，求GF的长；

(3)、以DD'为直径作⊙O．则在点E，F运动过程中，点E是否有可能恰好在⊙O上？若可能，求出a的值；若不可能，请说明理由．

查看试题解析