四川省资阳市安岳县2022-2023学年七年级上学期期末数学试卷
试卷更新日期:2023-01-14 类型:期末考试
一、选择题(本大题10个小题,每小题4分,共40分。)
-
1. ﹣ 的相反数是( )
A、﹣ B、 C、﹣2 D、22. 下列代数式中,次数是3的单项式是( )A、-a3b B、3a2b2 C、 D、3a3-33. 黄河是中华民族的母亲河,发源于巴颜喀拉山脉北麓,注入渤海,流域面积为750000km2 , 将数750000用科学记数法表示为( )A、7.5×104 B、75×104 C、75×105 D、7.5×1054. 下列正方体的展开图中,“手”的对面是“口”的展开图是( )A、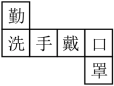 B、
B、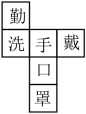 C、
C、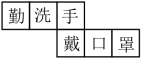 D、
D、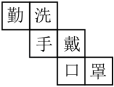 5. 下列判断中,正确的是( )A、-2是负数,但不是有理数 B、3a2bc与-bca2是同类项 C、8万与80000的精确度相同 D、多项式-x3+5x2y-3xy2+y3是按y的降幂排列6. 如图,下面说法正确的是( )
5. 下列判断中,正确的是( )A、-2是负数,但不是有理数 B、3a2bc与-bca2是同类项 C、8万与80000的精确度相同 D、多项式-x3+5x2y-3xy2+y3是按y的降幂排列6. 如图,下面说法正确的是( ) A、小红家在广场东偏北60°方向上,距离300米处 B、广场在学校南偏东35°方向上,距离200米处 C、广场在小红家东偏北30°方向上,距离300米处 D、学校在广场北偏西35°方向上,距离200米处7. 如图,若将三个含45°的直角三角板的直角顶点重合放置,若∠2=25°,∠3=35°,则∠1的度数为( )
A、小红家在广场东偏北60°方向上,距离300米处 B、广场在学校南偏东35°方向上,距离200米处 C、广场在小红家东偏北30°方向上,距离300米处 D、学校在广场北偏西35°方向上,距离200米处7. 如图,若将三个含45°的直角三角板的直角顶点重合放置,若∠2=25°,∠3=35°,则∠1的度数为( ) A、25° B、30° C、35° D、40°8. 按照如图所示的计算程序,若x=2,则输出的结果是( )
A、25° B、30° C、35° D、40°8. 按照如图所示的计算程序,若x=2,则输出的结果是( ) A、16 B、-16 C、26 D、-269. 下列说法:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若α=29°45′,则α的补角是150°55′;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )A、1个 B、2个 C、3个 D、4个10. 将连续正整数按如下规律排列:
A、16 B、-16 C、26 D、-269. 下列说法:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若α=29°45′,则α的补角是150°55′;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )A、1个 B、2个 C、3个 D、4个10. 将连续正整数按如下规律排列:第一列
第二列
第三列
第四列
第五列
第一行
1
2
3
4
第二行
8
7
6
5
第三行
9
10
11
12
第四行
16
15
14
13
第五行
17
18
19
20
…
若正整数2022位于第a行,第b列,则a+b的值为( )
A、507 B、508 C、509 D、510二、填空题(本大题6个小题,每小题4分,共24分。)
-
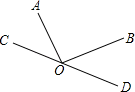
11. 化简:-|-3|= .12. 如图,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD= .
 13. 已知x+2y-3=0,则2x+4y-5= .14. 已知 ∠1的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为 .15. 定义新运算:求若干个相同的有理数(均不等于0)的商的运算叫做除方.比如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等,类比有理数的乘方,我们把2÷2÷2写作2③ , 读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)写作(-3)④ , 读作“(-3)的圈4次方”.一般地,把(a≠0)记作:aⓝ , 读作“a的圈n次方”.特别地,规定:a①=a.通过以上信息,请计算:2022②×(-)④+(-1)⑰= .16. 如图1,在长方形ABCD中,E点在AD上,并且∠ABE=26˚,分别以BE、CE为折痕进行折叠压平,如图2,若图2中∠AED=n°,则∠DEC的度数为 .
13. 已知x+2y-3=0,则2x+4y-5= .14. 已知 ∠1的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为 .15. 定义新运算:求若干个相同的有理数(均不等于0)的商的运算叫做除方.比如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等,类比有理数的乘方,我们把2÷2÷2写作2③ , 读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)写作(-3)④ , 读作“(-3)的圈4次方”.一般地,把(a≠0)记作:aⓝ , 读作“a的圈n次方”.特别地,规定:a①=a.通过以上信息,请计算:2022②×(-)④+(-1)⑰= .16. 如图1,在长方形ABCD中,E点在AD上,并且∠ABE=26˚,分别以BE、CE为折痕进行折叠压平,如图2,若图2中∠AED=n°,则∠DEC的度数为 .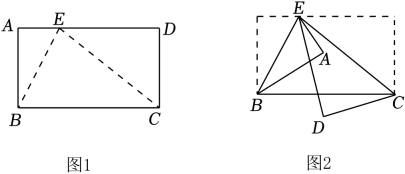
三、解答题(本大题共9个小题,共86分,)
-
17. 计算:(1)、12-(-18)+(-7)-|-20|;(2)、18. 先化简,再求值:3x2-[7x-2(5x-3)+(x2-x)],其中x2+2x-5=0.19. 如图是由7个小正方体(每个小正方体的棱长都是2dm)所堆成的几何体.
 (1)、请在相应方格纸中分别画出该几何体的主视图与俯视图;(2)、现要将这个几何体的表面上喷上油漆(不包括下底面),每平方分米的造价为5元,求漆完该几何体所需要的总费用为多少元?20. 填空并完成以下证明:
(1)、请在相应方格纸中分别画出该几何体的主视图与俯视图;(2)、现要将这个几何体的表面上喷上油漆(不包括下底面),每平方分米的造价为5元,求漆完该几何体所需要的总费用为多少元?20. 填空并完成以下证明:如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.

解:∠AED与∠C的大小关系是 .
证明:∵∠1+∠2=180°(已知)
∠1=∠DFH( )
∴ =180°
∴EH∥AB( )
∴∠3=∠ADE( )
∵∠3=∠B
∴∠B=∠ADE( )
∴ ∥BC( )
∴∠AED=∠C( )
21. 某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过的部分用正数来表示,不足的部分用负数来表示,记录如下:与标准质量的差值(单位:g)
-4
2
0
1
-3
5
袋数
3
5
3
4
2
3
(1)、这批样品的总质量比标准总质量多或少多少克?(2)、若每袋标准质量为450g,则抽样的平均质量为多少?22. 如图,用同样规格黑白两色的正方形瓷砖铺设长方形地面.请观察下列图形并解答有关问题: (1)、在第n个图中,第一横行共 块瓷砖,第一竖列共有 块瓷砖;(均用含n的代数式表示)(2)、在铺设第n个图形时,共用多少块瓷砖?(3)、若黑瓷砖每块15元,白瓷砖每块12元,当白砖共有10横行时,共需花多少钱购买瓷砖?23. 已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)、在第n个图中,第一横行共 块瓷砖,第一竖列共有 块瓷砖;(均用含n的代数式表示)(2)、在铺设第n个图形时,共用多少块瓷砖?(3)、若黑瓷砖每块15元,白瓷砖每块12元,当白砖共有10横行时,共需花多少钱购买瓷砖?23. 已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.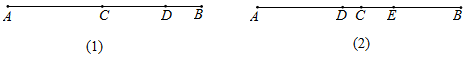 (1)、若 , 求线段CD的长度.(2)、若点E是线段AB上一点,且AE=2BE,当AD:BD=2:3时,求线段CD:CE的值24. 观察下列两个等式:2-=2×+1,5-=5×+1,给出定义如下:我们称使等a-b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),如数对(2,),(5,),都是“共生有理数对”.(1)、判断数对(3,)是否为“共生有理数对”,并说明理由;(2)、若(m,n)是“共生有理数对”,且mn=3,求(-2)m-n的值.(3)、若(m,-n)是“共生有理数对”,则(2n,-2m)是“共生有理数对”吗?请说明理由.25. 将一副三角板的两个锐角顶点重合,∠AOB=45°,∠COD=30°,OM、ON分别是∠AOC、∠BOD的平分线.
(1)、若 , 求线段CD的长度.(2)、若点E是线段AB上一点,且AE=2BE,当AD:BD=2:3时,求线段CD:CE的值24. 观察下列两个等式:2-=2×+1,5-=5×+1,给出定义如下:我们称使等a-b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),如数对(2,),(5,),都是“共生有理数对”.(1)、判断数对(3,)是否为“共生有理数对”,并说明理由;(2)、若(m,n)是“共生有理数对”,且mn=3,求(-2)m-n的值.(3)、若(m,-n)是“共生有理数对”,则(2n,-2m)是“共生有理数对”吗?请说明理由.25. 将一副三角板的两个锐角顶点重合,∠AOB=45°,∠COD=30°,OM、ON分别是∠AOC、∠BOD的平分线. (1)、如图1,当OB与OC重合时,则∠MON的大小为 ;(2)、当∠COD绕着点O旋转至如图2所示,且∠BOC=10°时,求∠MON的度数;(3)、当∠COD绕着点O旋转至如图3所示,且∠BOC=n°时,求∠MON的度数.
(1)、如图1,当OB与OC重合时,则∠MON的大小为 ;(2)、当∠COD绕着点O旋转至如图2所示,且∠BOC=10°时,求∠MON的度数;(3)、当∠COD绕着点O旋转至如图3所示,且∠BOC=n°时,求∠MON的度数.