四川省南充市顺庆区2022-2023学年九年级上学期摸底数学试卷（月考）

试卷更新日期：2023-01-14 类型：月考试卷

进入出卷网下载

一、选择题：本大题共10个小题，每小题4分，共40分.

1. 下列图案是轴对称图形，但不是中心对称图形的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 要使式子 $\frac{\sqrt{3 x + 9}}{x - 2}$ 有意义，x的取值范围是（）

A、x≥-3 B、x≥-3且x≠2 C、x＞-3且x≠2 D、x≤-3且x≠2

查看试题解析
3. 一组数据为7，9，9，11，若添加一个数据9，则发生变化的统计量是（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
4. 下列运算中，正确的是（）

A、5a⁶-a⁵＝4a B、a²⁰²³÷a²⁰²²＝a C、2a•5a⁴＝10a⁴ D、a²-4a-4＝（a-2）²

查看试题解析
5. 如图，在▱ABCD中，O为AC的中点，经过点O的直线交AD于E交BC于F，连接AF、CE，下列选项可以使四边形AFCE是菱形的为（）

A、OE＝OF B、AE＝CF C、EF⊥AC D、EF＝AC

查看试题解析
6. 把一元二次方程x²-6x-3＝0配方后可变形为（）

A、（x+3）²＝12 B、（x-3）²＝12 C、（x+3）²＝6 D、（x-3）²＝6

查看试题解析
7. 如图，△ABC的边AC经过⊙O的圆心O，BC与⊙O相切于B，D是⊙O上的一点，连接AD，BD，若∠C＝50°，则∠ADB的大小为（）

A、50° B、60° C、70° D、80°

查看试题解析
8. 若x＝-1是关于x的方程x²+ax+2b＝0的一个解，则（-2）^6b^-^3a＝（）

A、-8 B、- $\frac{1}{8}$ C、 $\frac{1}{8}$ D、6

查看试题解析
9. 如图，正方形OABC有三个顶点在抛物线y＝ $\frac{1}{4}$ x²上，点O是原点，顶点B在y轴上则顶点A的坐标是（）

A、（2，2） B、（ $\sqrt{2}$ ， $\sqrt{2}$ ） C、（4，4） D、（2 $\sqrt{2}$ ， 2 $\sqrt{2}$ ）

查看试题解析
10. 如图，在矩形ABCD中，AB＞AD，∠DAB的平分线与CD交于点E，过点C作CF⊥AE于点F，连接BF，DF．有下列结论：①DE＝BC；②DF＝BF；③∠CDF＝∠CBF；④B，C，D，F四点在同一个圆上．其中正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：本大题共6小题，每小题4分，共24分.

11. 若|-a|-|-9|＝0，则a＝．

查看试题解析
12. 在平面直角坐标系中，点M（a，1）与点N（3，b）关于原点对称，则a-b＝．

查看试题解析
13. 若将抛物线y＝- $\frac{1}{2}$ x²向左平移1个单位，再向下平移3个单位，则得到的抛物线的解析式是．

查看试题解析
14. 《九章算术》是中国古代第一部数学专著，它的出现标志着中国古代数学体系的形成．书中有如下问题：今有共买物，人出八，盈三：入出七，不足四．问人数、物价各几何？．大意是：有几个人一起去买一件物品，如果每人出8两，则多了3两：如果每人出7两，则少了4两，问有多少人？该物品价值多少两？若设该物品价值x两，根据题意，可列方程为．

查看试题解析
15. 如图，A，B，C三点都在⊙O上，已知∠AOC＝138°，则∠OAB+∠OCB＝°．

查看试题解析
16. 已知抛物线y＝ax²+bx+c（a≠0）经过点（-2，0），（0，4），对称轴在y轴右侧，有下列结论：
①a＜0；

②0＜b＜2；

③关于x的方程ax²+bx+c＝9始终有两个不等根；

④直线y＝ax+c（a≠0）与抛物线y＝ax²+bx+c（a≠0）始终有两个交点．

其中正确结论的序号为．

查看试题解析

三、解答题：本大题共9个小题，共86分。.

17. 解方程：

(1)、（x-3）（x+7）＝-16；

(2)、x²-1＝ $\frac{3}{2}$ x．

查看试题解析
18. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC，BC，BD．若CD＝2OE，求∠A和∠CBD的度数．

查看试题解析
19. 为了解某校学生上学的主要交通方式，校学生会设计了一份调查问卷，对该校部分学生进行了随机抽样调查．按A（骑自行车）、B（乘公交车）、C（步行）、D（乘私家车）、E（其他方式）设置选项，要求被调查同学从中单选，并将调查结果绘制成如下条形统计图．经统计，接受调查的同学中“骑自行车”的人数所占的百分比是15%．根据以上信息，解答下列问题：

(1)、本次接受调查的总人数是 ▲ 人，并把条形统计图补充完整；

(2)、若绘制扇形统计图，则“乘公交车”的人数所占的百分比是， “步行”选项所在扇形的圆心角度数是．

(3)、如果该校有学生3000人，请你求出该校学生大约多少人乘私家车上学．

查看试题解析
20. 关于x的一元二次方程为mx²-（1+2m）x+m+1＝0（m≠0）．

(1)、求证：方程总有两个不等实数根；

(2)、若方程的两根为x₁、x₂ ，是否存在x₁²+x₂²＝x₁x₂？如果存在，请求m的值；如果不存在，请说明理由．

查看试题解析
21. 如图，已知抛物线y＝ax²+bx+5（a≠0）的顶点为P（-3，-4）．

(1)、求抛物线的解析式；

(2)、抛物线与x轴交于点A，B，与y轴交于点C，求△ABC的面积．

查看试题解析
22. 如图，在△ABC中，∠BAC＝90°，以点A为圆心作⊙A与BC相切于D，交AB于点F，在BC上取点E，使CE＝AC，连接EA，EF．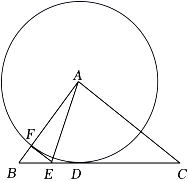

(1)、求证：EF是⊙A的切线；

(2)、若BE＝5，EF＝4，求点C到EA的距离．

查看试题解析
23. 某运动器材批发市场销售一种篮球，每个篮球进价为50元，规定每个篮球的售价不低于进价，经市场调查，每月的销售量y（个）与每个篮球的售价x（元）满足一次函数关系，部分数据如下表：

售价x

60

62

64

销售量y

500

480

460

(1)、求y与x之间的函数关系式；（不需求自变量x的取值范围）

(2)、该批发市场每月想从这种篮球销售中获利8000元，又想尽量多给客户实惠，应如何给这种篮球定价？

(3)、物价部门规定，该篮球的每个利润不允许高于进货价的50%，设销售这种篮球每月的总利润为w（元），那么销售单价定为多少元可获得最大利润？最大利润是多少？

查看试题解析
24. 如图，在正方形ABCD中，E是边CD上的一点，F是BD上的一点，且FE＝FC．

(1)、请你判断FE是否可以由FA旋转得到，如果可以，请说明旋转方向和角度并证明；如果不可以，请说明理由；

(2)、若正方形的边长为6 $\sqrt{3}$ +6，∠BAF＝30°．
（i）求AF的长度；

（ii）若AE与BD交于点G，求AG的长度．

查看试题解析
25. 如图，已知抛物线与x轴交于点A，B；与y轴交于点C，且OC＝OB＝2OA，对称轴为直线x＝1．

(1)、求抛物线的解析式．

(2)、若点M，N分别是线段AC，BC上的点，且MN∥AB，当MN＝2时，求点M，N的坐标．

(3)、D是抛物线的顶点，在抛物线上是否存在不与点D重合的点E，使得△BCE与△BCD的面积相等？若存在，请求点E的坐标；若不存在，请说明理由．

查看试题解析

售价x	60	62	64
销售量y	500	480	460