四川省达州市通川区六校联考2022-2023学年九年级上学期期末数学试卷
试卷更新日期：2023-01-14 类型：期末考试
一、选择题：本题共10小题，每小题4分，共40分。
-
1. 下列方程中，属于一元二次方程的是（ ）A、-3x+2＝0 B、2x2+y-1＝0 C、2x-3y+1＝0 D、x2-x-3＝02. 如果用□表示1个立方体，用
表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由6个立方体叠成的几何体，从正前方观察，可画出的平面图形是（ ）
A、
B、
C、
D、
3. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个面积为20cm2的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计试验结果），他将若干次有效试验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（ ）
A、6cm2 B、7cm2 C、8 cm2 D、9cm24. 下列性质中，平行四边形，矩形，菱形，正方形共有的性质是（ ）A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分内角5. 在反比例函数（k为常数）的图象上有三个点（-3，y1），（-1，y2）， ， 则函数值y1 ， y2 ， y3的大小关系为（ ）A、y1＜y2＜y3 B、y1＜y3＜y2 C、y2＜y3＜y1 D、y3＜y1＜y26. 如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段AB＝3，则线段BC的长是（ ）
A、 B、1 C、 D、27. 如图，EB为驾驶员的盲区，驾驶员的眼睛点P处与地面BE的距离为1.6米，车头FACD近似看成一个矩形，且满足3FD＝2FA，若盲区EB的长度是6米，则车宽FA的长度为（ ）米．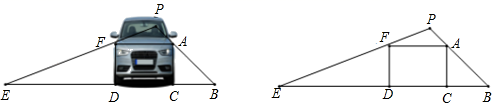
A、 B、 C、 D、28. 设x1 ， x2是一元二次方程x2+x-3＝0的两根，则x13-4x22+20等于（ ）A、1 B、5 C、11 D、139. 如图，在平面直角坐标系xOy中，△ABC与△ODE是位似图形，则它们的位似中心的坐标是（ ）
A、（4，4） B、（4，3） C、（4，2） D、（3，4）10. 如图是4个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作Tm（m为1～4的整数），函数y＝（x＞0）的图象为曲线L．若曲线L使得T1～T4 ， 这些点分布在它的两侧，每侧各2个点，则k的取值范围是（ ）
A、8≤k≤12 B、8≤k＜12 C、8＜k≤12 D、8＜k＜12二、填空题：本题共5小题，每小题6分，共30分。
-
11. 大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是9cm，则蜡烛火焰的高度是 cm．
12. 方程x2-6x+8＝0的两个根是等腰三角形的底和腰，则这个等腰三角形周长是 ．13. 如图，E是△ABC的中线AD上一点，CE的延长线交AB于点F，若AF＝2，ED＝3AE，则AB的长为 ．
14. 如图，在平面直角坐标系中，点A的坐标是（5，0），函数y＝（x＞0）的图象经过菱形OABC的顶点C，若OB•AC＝40，则k的值为 ．
15. 如图，已知矩形ABCD中，AB＝3，BC＝4，点M，N分别在边AD，BC上，沿着MN折叠矩形ABCD，使点A，B分别落在E，F处，且点F在线段CD上（不与两端点重合），过点M作MH⊥BC于点H，连接BF，给出下列判断：①△MHN∽△BCF；
②折痕MN的长度的取值范围为3＜MN＜；
③当四边形CDMH为正方形时，N为HC的中点；
④若DF＝DC，则折叠后重叠部分的面积为 ．
其中正确的是 ． （写出所有正确判断的序号）
三、解答题：共80分。解答应写出文字说明、证明过程或演算步骤。
-
16. 解方程：(1)、x2-x-＝0；(2)、x（x-4）＝8-2x．17. 如图，在直角坐标系中，已知△ABC三个顶点的坐标分别为A（3，3），B（4，0），C（0，2）．
(1)、以点O为位似中心，将△ABC缩小为原来的 ， 得到△A1B1C1 ， 请在y轴的右侧画出△A1B1C1 ．(2)、在y轴上是否存在点P，使得|B1P-A1P|的值最大，若存在，请求出满足条件的点P的坐标；若不存在，请说明理由．18. 为提高教育质量，落实立德树人的根本任务，中共中央办公厅、国务院办公厅颁布了“双减”政策．为了调查学生对“双减”政策的了解程度，某学校数学兴趣小组通过网上调查的方式在本校学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查结果，绘制了如图的统计图，结合统计图，回答下列问题：
(1)、若该校有学生2000人，请根据调查结果估计这些学生中“比较了解”“双减”政策的人数约为多少？(2)、根据调查结果，学校准备开展关于“双减”政策宣传工作，要从某班“非常了解”的小明和小刚中选一个人参加，现设计了如下游戏来确定，具体规则是：在一个不透明的袋中装有2个红球和2个白球，它们除了颜色外无其他差别，从中随机摸出两个球，若摸出的两个球颜色相同，则小明去；否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．19. 在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
(1)、证明：四边形ADCF是菱形；(2)、若AC＝3，AB＝4，求菱形ADCF的面积．20. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳，如图是小然站在地面MN欣赏悬挂在墙壁PM上的油画AD（PM⊥MN）的示意图，设油画AD与墙壁的夹角∠PAD＝α，此时小然的眼睛与油画底部A处于同一水平线上，视线恰好落在油画的中心位置E处，且与AD垂直．已知油画的长度AD为100cm．
(1)、视线∠ABD的度数为 .（用含α的式子表示）(2)、当小然到墙壁PM的距离AB＝250cm时，求油画顶部点D到墙壁PM的距离．21. 为了满足社区居民强身健体的需要，政府准备采购若干套健身器材免费提供给社区，经过考察了解，飞跃公司有A，B两种型号的健身器材可供选择，已知飞跃公司2020年每套A型健身器材的售价为2.5万元，2020年每套B型健身器材的售价为2万元，2022年每套A型健身器材售价为1.6万元，每套A型，B型健身器材的年平均下降率相同．(1)、求2020年到2022年每套A型健身器材年平均下降率；(2)、2022年政府经过招标，决定年内采购并安装飞跃公司A，B两种型号的健身器材共80套，政府采购专项经费总计不超过115.2万元，并且采购A型器材费用不能少于B型器材的费用，请求出所需经费最少的采购方案．22. 如图，一次函数y＝k1x+b（k≠0）与反比例函数y＝）的图象交于A（1，6），B（3，m）两点．
(1)、求反比例函数和一次函数的解析式；(2)、根据图象直接写出k1x+b＜时，x的取值范围；(3)、求△AOB的面积．23. 如图，正方形ABCD的对角线相交于点O．点E是线段DO上一点，连接CE．点F是∠OCE的平分线上一点，且BF⊥CF与CO相交于点G．点H是线段CE上一点，且CO＝CH．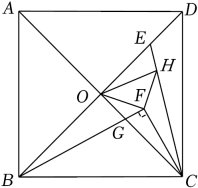
(1)、若OF＝5，求FH的长；(2)、求证：BF＝OH+CF．24. 配方法是数学中非常重要的一种思想方法，它是指将一个式子或将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法，这种方法常被用到代数式的变形中，并结合非负数的意义来解决问题．定义：若一个整数能表示成a2+b2（a，b为整数）的形式，则称这个数为“完美数”．
例如，5是“完美数”，理由：因为5＝12+22 ， 所以5是“完美数”．
解决问题：
(1)、已知29是“完美数”，请将它写成a2+b2（a，b为整数）的形式；(2)、若x2-4x+5可配方成（x-m）2+n（m，n为常数），求mn的值；(3)、已知S＝x2+4y2+4x-12y+k（x，y是整数，k是常数），要使S为“完美数”，试求出k值．25. 如图
(1)、如图1，点E在正方形ABCD内，且在对角线AC上方，连接AE，CE，EF⊥AE，以EF，EC为邻边作平行四边形ECGF，连接ED，EG，DG．当AE＝EF时，试探究ED与EG之间的数量关系并说明理由；(2)、如图2，点E在矩形ABCD内，且在对角线AC右侧，连接AE，CE，EF⊥AE，以EF，EC为邻边作平行四边形ECGF，连接ED，EG，DG，当AE＝EF，且AD：DC＝3：2，求ED：EG的值．