初中数学同步训练必刷题(北师大版七年级下册 第二章 相交线与平行线 全章测试卷 )
试卷更新日期:2023-01-14 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 下列图形中,∠1与∠2是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在同一平面内,不重合的两条直线可能的位置关系是( )A、平行 B、相交 C、平行或相交 D、不能确定3. 若 , 则的余角的补角为( )A、20° B、70° C、110° D、160°4. 如图,下列条件中,不能判断直线l1∥l2的是( )
2. 在同一平面内,不重合的两条直线可能的位置关系是( )A、平行 B、相交 C、平行或相交 D、不能确定3. 若 , 则的余角的补角为( )A、20° B、70° C、110° D、160°4. 如图,下列条件中,不能判断直线l1∥l2的是( ) A、 B、 C、 D、5. 如图,直线和被直线所截,则( )
A、 B、 C、 D、5. 如图,直线和被直线所截,则( ) A、和是同位角 B、和是内错角 C、和是同位角 D、和是内错角6. 如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是( )A、∠3>∠4 B、∠3=∠4 C、∠3<∠4 D、不确定7. 如图,已知 , 那么下列结论一定正确的是( )
A、和是同位角 B、和是内错角 C、和是同位角 D、和是内错角6. 如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是( )A、∠3>∠4 B、∠3=∠4 C、∠3<∠4 D、不确定7. 如图,已知 , 那么下列结论一定正确的是( ) A、 B、 C、 D、8.
A、 B、 C、 D、8.如图,已知:AB∥CD,CE分别交AB、CD于点F、C,若∠E=20°,∠C=45°,则∠A的度数为( )
 A、5° B、15° C、25° D、35°9. 如图,AB∥CD,直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为( )
A、5° B、15° C、25° D、35°9. 如图,AB∥CD,直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为( ) A、28° B、62° C、56° D、72°10. 如图(1)是一段长方形纸带, , 将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数为( )
A、28° B、62° C、56° D、72°10. 如图(1)是一段长方形纸带, , 将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数为( )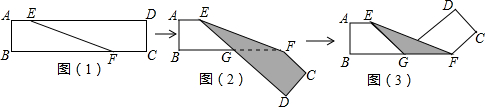 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共30分)
-
11. 如图,直线a,b相交于点O,∠1=130°,则∠2的度数是 .
 12. 如图,与 是内错角的是.
12. 如图,与 是内错角的是.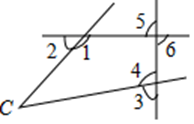 13. 如果一个角的补角是115°,那么这个角的余角的度数是 .14. 若 , , 则 . (填>、<、=)15. 如图,在不添加辅助线及字母的前提下,请写出一个能判定 的条件:.
13. 如果一个角的补角是115°,那么这个角的余角的度数是 .14. 若 , , 则 . (填>、<、=)15. 如图,在不添加辅助线及字母的前提下,请写出一个能判定 的条件:. 16. 如图所示,∠A=60°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,则直线OD绕点O按逆时针方向至少要旋转度.
16. 如图所示,∠A=60°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,则直线OD绕点O按逆时针方向至少要旋转度. 17. 如图,直线ab,直线AB分别与直线a,b相交于点C和点B,过点C作射线CD⊥AB于C,若∠1=57°,则∠2的度数是 .
17. 如图,直线ab,直线AB分别与直线a,b相交于点C和点B,过点C作射线CD⊥AB于C,若∠1=57°,则∠2的度数是 . 18. 如图, , 直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= .
18. 如图, , 直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= . 19. 如图,ABCD , 直线交于点O,过O作 , 交于点G, , 则°.
19. 如图,ABCD , 直线交于点O,过O作 , 交于点G, , 则°. 20. 如图,直线m∥n,一副直角三角板按如图所示放置,若 , , , 则的度数等于 .
20. 如图,直线m∥n,一副直角三角板按如图所示放置,若 , , , 则的度数等于 .
三、解答题(共6题,共60分)
-
21. 如图,点 , 点 , 点均在格点上,且点C在的边上.
 (1)、过点画的垂线交于点;(2)、过点画的平行线,交(1)中所画垂线于点 , 连接;(3)、点到直线的距离是图中哪条线段的长度?22. 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF , ∠C=∠D , 可以证明∠A=∠F . 请完成下面证明过程中的各项“填空”.
(1)、过点画的垂线交于点;(2)、过点画的平行线,交(1)中所画垂线于点 , 连接;(3)、点到直线的距离是图中哪条线段的长度?22. 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF , ∠C=∠D , 可以证明∠A=∠F . 请完成下面证明过程中的各项“填空”.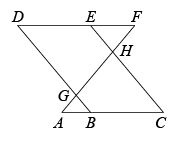
证明:∵∠AGB=∠EHF(已知),∠AGB=∠DGF( )
∴∠EHF=∠DGF , ∴( )
∴∠C=∠DBA( )
又∵∠C=∠D , ( )∴∠DBA=∠D , ( )
∴( )
∴∠A=∠F( ).
23. 已知:如图,点在一条直线上,与交于点 , , CMDN . 求证: . 24. 如图,已知 , , 于点 , 那么与有什么数量关系?为什么?
24. 如图,已知 , , 于点 , 那么与有什么数量关系?为什么?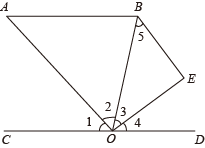 25. 已知射线(M,N在射线CA的右侧),点B在射线AM上,点D在射线CN上,点E在射线CA上(不与点A重合),且满足∠BAC+∠BED=180°.
25. 已知射线(M,N在射线CA的右侧),点B在射线AM上,点D在射线CN上,点E在射线CA上(不与点A重合),且满足∠BAC+∠BED=180°. (1)、如图1,点E在线段AC上.
(1)、如图1,点E在线段AC上.①若∠BED=60°,∠ABE=20°,求∠CDE的度数.
②探究∠CDE与∠AEB的数量关系,并说明理由.
(2)、设 , , ∠AEB与∠EDN的平分线交于点P,请用的代数式表示∠EPD的度数.26. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.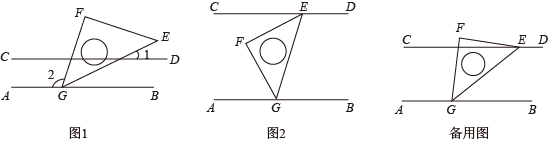 (1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.
(1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.