初中数学同步训练必刷题(北师大版七年级下册2.4 用尺规作角)
试卷更新日期:2023-01-14 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列图形中,能确定 的是( )A、
 B、
B、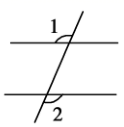 C、
C、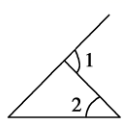 D、
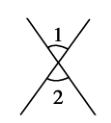
D、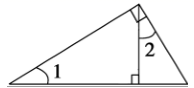 2. 则与的关系是( )A、 B、 C、 D、以上都不对3. 下列各图中,∠与∠是一定相等的是( )A、
2. 则与的关系是( )A、 B、 C、 D、以上都不对3. 下列各图中,∠与∠是一定相等的是( )A、 B、
B、 C、
C、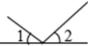 D、
D、 4. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β一定相等的图形个数共有( )
4. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β一定相等的图形个数共有( ) A、1个 B、2个 C、3个 D、4个5. 如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )
A、1个 B、2个 C、3个 D、4个5. 如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )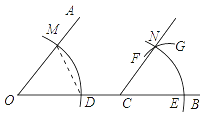 A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧6. 下列说法不正确的是( )A、角的大小与角的边画出部分的长短无关 B、角的大小与它们度数的大小是一致的 C、角的平分线是一条线段 D、角的和、差、倍、分的度数等于它们度数的和、差、倍、分7. 已知∠1=38°36′,∠2=38.36°,∠3=38.6°, 则下列说法正确的是( )A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠1、∠2、∠3互不相等8. 通过下面几个图形说明“锐角α,锐角β的和是锐角”,其中错误的例证图是( )A、
A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧6. 下列说法不正确的是( )A、角的大小与角的边画出部分的长短无关 B、角的大小与它们度数的大小是一致的 C、角的平分线是一条线段 D、角的和、差、倍、分的度数等于它们度数的和、差、倍、分7. 已知∠1=38°36′,∠2=38.36°,∠3=38.6°, 则下列说法正确的是( )A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠1、∠2、∠3互不相等8. 通过下面几个图形说明“锐角α,锐角β的和是锐角”,其中错误的例证图是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,点在的边上,用尺规作出了.以下是排乱的作图过程:
9. 如图,点在的边上,用尺规作出了.以下是排乱的作图过程:①以为圆心,长为半径画 , 交于点.
②作射线 , 则.
③以为圆心,长为半径画弧,交于点.
④以为圆心,任意长为半径画 , 分别交 , 于点 , .则正确的作图顺序是( )
 A、①—②—③—④ B、③—②—④—① C、④—①—③—② D、④—③—①—②10. 如图所示,O是直线AB上一点,图中小于180°的角共有( )
A、①—②—③—④ B、③—②—④—① C、④—①—③—② D、④—③—①—②10. 如图所示,O是直线AB上一点,图中小于180°的角共有( ) A、7个 B、9个 C、8个 D、10个
A、7个 B、9个 C、8个 D、10个二、填空题(每空3分,共33分)
-
11. 若 , , 则 . (填>、<、=)12. 如图,直线AB,CD交于点O, ,现作射线OE⊥CD,则∠AOE的大小为.
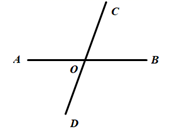 13. 如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=°.
13. 如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=°. 14. 已知∠AOB和∠COD的两边分别互相垂直,且∠COD比∠AOB的3倍少60°,则∠COD的度数为15. 如图,在 中, , , ,则 .
14. 已知∠AOB和∠COD的两边分别互相垂直,且∠COD比∠AOB的3倍少60°,则∠COD的度数为15. 如图,在 中, , , ,则 . 16. 如图,AOB为一直线,OC,OD,OE是射线,则图中大于0°小于180°的角有个.
16. 如图,AOB为一直线,OC,OD,OE是射线,则图中大于0°小于180°的角有个.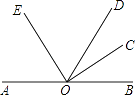 17. 根据图,比较∠AOC,∠BOD,∠BOC,∠COD,∠AOD的大小,它们从小到大排列为 .
17. 根据图,比较∠AOC,∠BOD,∠BOC,∠COD,∠AOD的大小,它们从小到大排列为 . 18. 如果∠1=∠2,∠2=∠3,则∠1∠3;如果∠1>∠2,∠2>∠3,则∠1∠3.19. 如果∠1=70°,∠2=120°,∠3=89°,那么它们的大小关系是(用<连接)20. 已知OA⊥OB,∠AOC∶∠AOB=2∶3,则∠BOC的度数为°.
18. 如果∠1=∠2,∠2=∠3,则∠1∠3;如果∠1>∠2,∠2>∠3,则∠1∠3.19. 如果∠1=70°,∠2=120°,∠3=89°,那么它们的大小关系是(用<连接)20. 已知OA⊥OB,∠AOC∶∠AOB=2∶3,则∠BOC的度数为°.三、解答题(共6题,共57分)
-
21.
如上如图所示,求作一个角等于已知角∠AOB.
作法:(1)作射线;
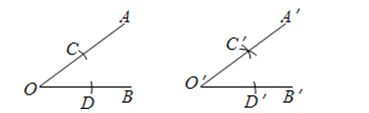
(2)以 为圆心,以为半径画弧,交OA于点C,交OB于点D;
(3)以为圆心,以为半径画弧,交O′B′于点D′;
(4)以点D′为圆心,以为半径画弧,交前面的弧于点C′;
(5)过作射线O′A′.∠A′O′B′就是所求作的角.
22. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=70°,求∠BOM的值.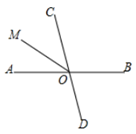 23. 如图所示,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=50°,求∠BOF的度数.
23. 如图所示,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=50°,求∠BOF的度数. 24. 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°.求∠COD的度数.
24. 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°.求∠COD的度数.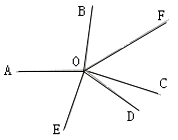 25. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°)
25. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°) (1)、①若 ∠DCE=45°,求∠ACB;
(1)、①若 ∠DCE=45°,求∠ACB;②若∠ACB=140°,求∠DCE ;
(2)、由(1)猜想 ∠ACB与∠DCE的数量关系,并说明理由;(3)、这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE的所有可能的值(不必说明理由);若不存在,请说明理由.
26. 如图,已知AB∥CD. (1)、判断∠FAB与∠C的大小关系,请说明理由;(2)、若∠C=35°,AB是∠FAD的平分线.
(1)、判断∠FAB与∠C的大小关系,请说明理由;(2)、若∠C=35°,AB是∠FAD的平分线.①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.