人教版九年级数学2023年寒假专项训练----预习部分相似三角形的应用举例

试卷更新日期：2023-01-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，为估算学校的旗杆的高度，身高 $1.6$ 米的小红同学沿着旗杆在地面的影子 $A B$ 由 $A$ 向 $B$ 走去，当她走到点 $C$ 处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得 $A C = 2 m$ ， $B C = 8 m$ ，则旗杆的高度是（）

A、6.4m B、7m C、8m D、9m

查看试题解析
2. 如图，圆桌正上方的灯泡O发出的光线照射桌面后，在地面上形成圆形阴影.已知桌面的直径为1.2m，桌面距离地面1m，若灯泡O距离地面3m，则地面上阴影部分的面积为（）

A、0.36πm² B、0.81πm² C、1.44πm² D、3.24πm²

查看试题解析
3. 《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中的第一问：今有望海岛，立两表，齐高三丈，前后相去千步，令后表与前表参相直.从前表却行一百二十三步，人目着地取望岛峰，与表末参合.从后表却行一百二十七步，人目着地取望岛峰，亦与表末参合.问岛高及去表各几何？大致意思是：假设测量海岛，立两根表，高均为3丈，前后相距1000步，令后表与前表在同一直线上，从前表退行123步，人的眼睛贴着地面观察海岛，从后表退行127步，人的眼睛贴着地面观察海岛，问海岛高度及两表相距多远？想要解决这一问题，需要利用（）

A、全等三角形 B、相似三角形 C、勾股定理 D、垂径定理

查看试题解析
4. 如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m远，该同学的身高为1.7m，则树高为（）m.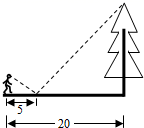

A、3.4 B、5.1 C、6.8 D、8.5

查看试题解析
5. 如图所示为我市某农村一古老的捣碎器，已知支撑柱AB的高为0.3米，踏脚着地时捣头点E距离地面0.8米，则捣头点E着地时，踏脚点D距离地面（）

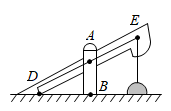A、0.4 米 B、0.48米 C、0.5 米 D、0.8米

查看试题解析
6. 我国古代数学著作《九章算术》中的“井深”问题：“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”，它的题意是：如图 $A B = D E = 5$ 尺， $B F = 0.4$ 尺，问井深 $B D$ 是多少．如图，设井深为x尺，所列方程正确的是（）

A、 $\frac{5}{5 + x} = \frac{0.4}{5}$ B、 $\frac{5}{x} = \frac{0.4}{5}$ C、 $\frac{x}{5 + x} = \frac{5}{0.4}$ D、 $\frac{5}{x} = \frac{5 - 0.4}{0.4}$

查看试题解析
7. 如图，有一块锐角三角形材料，边BC＝120mm ，高AD＝90mm ，要把它加工成矩形零件，使其一边在BC上，其余两个顶点分别在AB ， AC ，且EH＝2EF ，则这个矩形零件的长为（）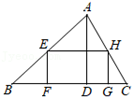

A、36mm B、80mm C、40mm D、72mm

查看试题解析

二、填空题

8. 如图，在 $△ A B C$ 中， $∠ C = 9 0^{∘}$ ， $A C = 30 c m$ ， $B C = 25 c m$ ，动点P从点C出发，沿 $C A$ 方向运动，速度是 $2 c m / s$ ；动点Q从点B出发，沿 $B C$ 方向运动，速度是 $1 c m / s$ ，若P、Q同时出发，点P运动到点A时，P、Q两点同时停止运动，在s时， $△ A B C$ 与 $△ P Q C$ 相似.

查看试题解析
9. 如图，小红晚上由路灯A下的B处走到C处时，测得影子 $C D$ 的长为1米，继续往前走2.5米到达E处时，测得影子EF的长为2米，已知小明的身高是1.5米，那么路灯A离地面的高度 $A B$ 的长为米．

查看试题解析
10. 如图，利用标杆DE测量楼高，点A、D、B在同一条直线上，DE⊥AC，BC⊥AC，垂足分别为E、C．若测得AE＝1m，DE＝1.5m，CE＝5m，则楼高BC为m．

查看试题解析
11. 《九章算术》中记载了一种测量井深的方法．如图所示，在井口 $B$ 处立一根垂直于井口的木杆 $B D$ ，从木杆的顶端 $D$ 观察井水水岸 $C$ ，视线 $D C$ 与井口的直径 $A B$ 交于点 $E$ ，如果测得 $A B = 1.6$ 米， $B D = 1$ 米， $B E = 0.2$ 米，那么井深 $A C$ 为米．

查看试题解析
12. 如图，正方形城邑 $D E F G$ 的四面正中各有城门，出北门20步的A处（ $H A = 20$ 步）有一树木，由南门14步到C处（ $K C = 14$ 步），再向西行1775步到B处（ $C B = 1775$ 步），正好看到A处的树木（点D在直线 $A B$ 上），则城邑的边长为步．

查看试题解析
13. 如图1所示的是古代一种可以远程攻击的投石车，图2是投石车投石过程中某时刻的示意图， $G P$ 是杠杆，弹袋挂在点 $G$ ，重锤挂在点 $P$ ，点 $A$ 为支点，点 $D$ 是水平底板 $B C$ 上的一点， $A D = A C = 3$ 米， $C D = 3.6$ 米．

(1)、投石车准备时，点 $G$ 恰好与点 $B$ 重合，此时 $A G$ 和 $A C$ 垂直，则 $B D =$ 米．

(2)、投石车投石过程中， $A P$ 的延长线交线段 $D C$ 于点 $E$ ，若 $D E$ ： $C E = 5$ ： $1$ ，则点 $G$ 距地面为米．

查看试题解析

人教版九年级数学2023年寒假专项训练----预习部分 相似三角形的应用举例

一、单选题

二、填空题

人教版九年级数学2023年寒假专项训练----预习部分相似三角形的应用举例