初中数学同步训练必刷题(人教版八年级下册 第十七章 勾股定理 全章测试卷)
试卷更新日期:2023-01-13 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 一个直角三角形的两条边的长分别为8,10,则第三条边的长为( )A、6 B、12 C、 D、6或2. 下列各组数中,是勾股数的是( )A、1, , 3 B、0.3,0.4,0.6 C、9,12,15 D、5,6,73. 在边长为1的小正方形组成的网格中,A,B,C,D、E在格点上,长度是的线段是( )
 A、AB B、AC C、AD D、AE4. 如图,某公园的一块草坪旁边有一条直角小路,公园管理处为了方便群众,沿修了一条近路,已知米,米,则走这条近路可以少走( )米路
A、AB B、AC C、AD D、AE4. 如图,某公园的一块草坪旁边有一条直角小路,公园管理处为了方便群众,沿修了一条近路,已知米,米,则走这条近路可以少走( )米路 A、30 B、20 C、50 D、405. 如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:),可以计算出两圆孔中心B和C的距离为( ) .
A、30 B、20 C、50 D、405. 如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:),可以计算出两圆孔中心B和C的距离为( ) . A、120 B、135 C、 D、1506. 如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为( )
A、120 B、135 C、 D、1506. 如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为( ) A、1 B、 C、 D、7. 斜边长是4的直角三角形,它的两条直角边可能是( )A、3, B、2,3 C、3,5 D、2,28. 在中,∠A,∠B,∠C的对边分别是a,b,c,下列条件中,不能判定是直角三角形的是( )A、 B、 C、 , , D、 , ,9. 如图,有一架秋千,当它静止时,踏板离地0.5米,将它往前推3米时,踏板离地1.5米,此时秋千的绳索是拉直的,则秋千的长度是( )
A、1 B、 C、 D、7. 斜边长是4的直角三角形,它的两条直角边可能是( )A、3, B、2,3 C、3,5 D、2,28. 在中,∠A,∠B,∠C的对边分别是a,b,c,下列条件中,不能判定是直角三角形的是( )A、 B、 C、 , , D、 , ,9. 如图,有一架秋千,当它静止时,踏板离地0.5米,将它往前推3米时,踏板离地1.5米,此时秋千的绳索是拉直的,则秋千的长度是( ) A、3米 B、4米 C、5米 D、6米10. 如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A、3米 B、4米 C、5米 D、6米10. 如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )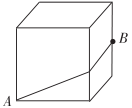 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共30分)
-
11. 如图的直角三角形中未知边的长x=.
 12. 一个直角三角形的两直角边长分别为2,4,则斜边长为.13. 一艘船以20海里/时的速度从A港向东北方向航行,另一艘船以15海里/时的速度从A港向西北方向航行,经过1小时后,它们相距海里.14. 如图,直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C,且相互平行,若L1、L2的距离为1,L2、L3的距离为2,则正方形的边长为 .
12. 一个直角三角形的两直角边长分别为2,4,则斜边长为.13. 一艘船以20海里/时的速度从A港向东北方向航行,另一艘船以15海里/时的速度从A港向西北方向航行,经过1小时后,它们相距海里.14. 如图,直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C,且相互平行,若L1、L2的距离为1,L2、L3的距离为2,则正方形的边长为 .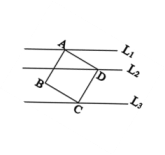 15. 如图所示,点B,D在数轴上 , , , 以D为圆心,DC长为半径画弧,与数轴正半轴交于点A,则点A表示的实数是 .
15. 如图所示,点B,D在数轴上 , , , 以D为圆心,DC长为半径画弧,与数轴正半轴交于点A,则点A表示的实数是 .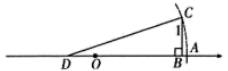 16. 在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 .
16. 在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 . 17. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.
17. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米. 18. 在 中,高 ,若 , ,则 的面积为.19. 如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是.
18. 在 中,高 ,若 , ,则 的面积为.19. 如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是. 20. 如图,长方体的长为 ,宽为 ,高为 ,点 距离 点 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,则蚂蚁爬行的最短距离是 .
20. 如图,长方体的长为 ,宽为 ,高为 ,点 距离 点 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,则蚂蚁爬行的最短距离是 .
三、解答题(共6题,共60分)
-
21. 如图,在△ABC中,AE=3,BE=5,AC=4,DE是BC的垂直平分线,交BC于点D,交AB于点E.求证:△ABC为直角三角形.
 22. 某船从港口A出发沿南偏东32°方向航行12海里到达B岛,然后沿某方向航行16海里到达C岛,最后沿某个方向航行了20海里回到港口A,则该船从B到C是沿哪个方向航行的?(即求C岛在B岛的哪个方位,距离B岛多远?),请说明理由.
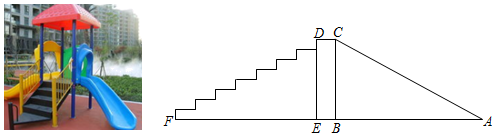
22. 某船从港口A出发沿南偏东32°方向航行12海里到达B岛,然后沿某方向航行16海里到达C岛,最后沿某个方向航行了20海里回到港口A,则该船从B到C是沿哪个方向航行的?(即求C岛在B岛的哪个方位,距离B岛多远?),请说明理由.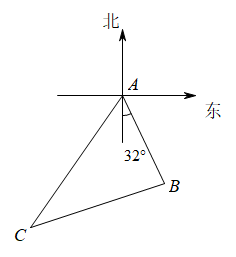 23. 滑梯的示意图如图所示,左边是楼梯,右边是滑道,立柱 , 垂直于地面 , 滑道的长度与点A到点E的距离相等,滑梯高 , 且 , 求滑道的长度.
23. 滑梯的示意图如图所示,左边是楼梯,右边是滑道,立柱 , 垂直于地面 , 滑道的长度与点A到点E的距离相等,滑梯高 , 且 , 求滑道的长度.